Calcul de limites en un réel

Bonjour, Pouvez-m'aider à résoudre cet exercice svp ?
Voici l'énoncé : Lève les indéterminations suivantes après avoir recherché le domaine de la fonction, précise si les limites sont des limites à gauche, à droite ou les deux. :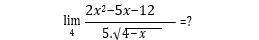 2021-05-02 (2).png

@Joyca-Le-Boss Bonjour,

As-tu déterminé le domaine de définition ?
Factorise le numérateur.

@Noemi le Numérateur vaut : ( x - 4 ).( x + 3/2)

@Joyca-Le-Boss

Il manque un coefficient 2 devant.

Calcule les limites.

@Noemi N(4) = 0
D(4) = 0
Je dois donc factoriser et multiplier le numérateur et le dénominateur par racine de 4-x .
Est-ce correct ?

@Noemi Est-ce correct ?

Bonjour,

@Joyca-Le-Boss , tu aurais dû répondre à la premiere question de Noemi "As-tu déterminé le domaine de définition"

Tu saurais ainsi quelle limite il faut chercher : à droite ou à gauche (ou les deux)

Condition : $\gt 0$ <=> $x<4x\lt 4$

$Df=]−∞,4[D_f=]-\infty, 4[$

Tu cherches donc la limite à gauche

Avec ta factorisation du numérateur, tu peux écrire :

$f(x)=−2(4−x)(x+32)54−xf(x)=\dfrac{-2(4-x)(x+\dfrac{3}{2})}{5\sqrt{4-x}}$

Tu simplifies par $4−x\sqrt{4-x}$ et tu cherches la limite de l'expression simplifiée

@mtschoon ou est allé le 5 de racine de 4-x svp ?

@Joyca-Le-Boss ,

Le 5 avait disparu car je ne l'avais pas vu.
Je viens de le remettre.

Donne l'expression simplifiée et la limite que tu as trouvée si tu souhaites une vérification.

@Joyca-Le-Boss ,

Une piste si ça t'arrange pour la simplification

Pense que pour tout réel a positif : $a=a×aa=\sqrt a \times \sqrt a$ , c'est à dire ici : $4−x=4−x×4−x4-x=\sqrt{4-x}\times \sqrt{4-x}$

Tu dois trouver 0 comme limite ( à gauche).

Reposte si tu n'y arrives pas.

@mtschoon J'ai pas compris d'où sort le zéro

Ce message a été supprimé !

@Joyca-Le-Boss ,

Le "zéro" est la limite que tu dois trouver.

Si tu as fait la simplification par $4−x\sqrt{4-x}$ , tu as dû trouver :
$f(x)=−25(4−x)(x+32)f(x)=-\dfrac{2}{5}(\sqrt{4-x})(x+\dfrac{3}{2})$

Il te reste à faire tendre x vers 4 dans chaque facteur.

@mtschoon on trouve donc 0/5 donc 0 si on remplace X par 4

@Joyca-Le-Boss ,

OUI, mais mathématiquement, on ne "remplace pas x par 4" on donne à x des valeurs s'approchant de 4 (c'est à dire tendant vers 4).
C'est ça la notion de limite.

@mtschoon ok merci pouvez m'aidez pour les 2 autres svp !

@Joyca-Le-Boss , re-bonjour,
Bien sûr que je peux t'aider pour tes deux autres exercices sur les limites.
Je vais regarder, mais je pense que tu as déjà des réponses.