Calculs de limites de fonctions avec une fraction et une racine carrée

[Joyca Le Boss]

Bonjour ,Pouvez m'aidez a résoudre cet exercice c'est sur les limites
voici l'énoncé : Lève les indéterminations suivantes après avoir recherché le domaine de la fonction, précise si les limites sont des limites à gauche, à droite ou les deux.

[Noemi]

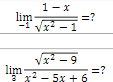
@Joyca-Le-Boss Bonjour,

Applique le même raisonnement que pour l'autre sujet.
Indique tes éléments de réponse.

[Joyca Le Boss]

@Noemi ok

[Joyca Le Boss]

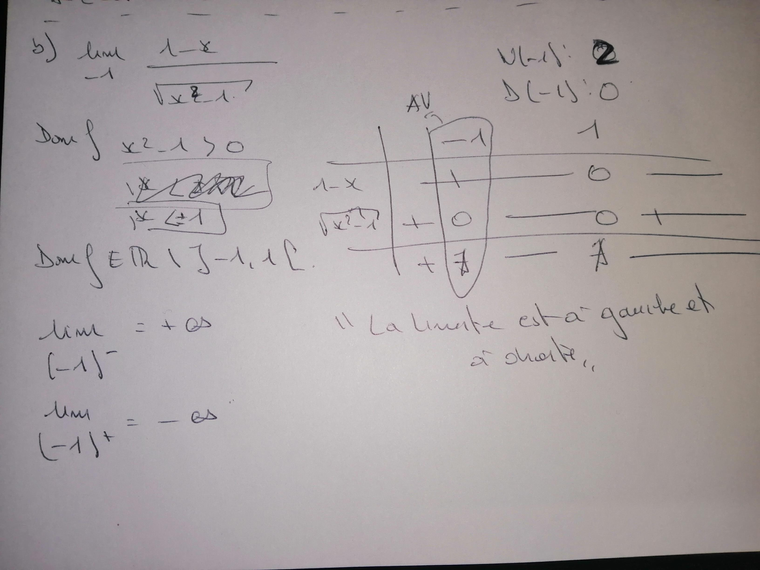
@Noemi Voici mon raisonnement : Est-ce correct ?

[Noemi]

@Joyca-Le-Boss

Pas très clair ce document surtout la partie de droite.

$-1^{+}$ n'appartient pas au domaine de définition.
La limite en $-1^{-}$ est correcte

Calcule la limite en $1^{+}$.

[mtschoon]

Bonjour,

@Joyca-Le-Boss ,

Effectivement ton "brouillon" n'est guère clair...

Vérifie l'ensemble de définition.

$x^2-1>0$ <=> $x<-1$ ou $x>1$

-1 et 1 ne font pas partie de l'ensemble de définition.
S'ils en faisaient partie, on ne chercherait pas les limites.
On calculerait f(-1) et f(1).

$D=]-\infty ,-1[\cup ]1,+\infty [$
Si tu préfères, $\boxed{D=R/[-1,1]}$

Vu le domaine, comme te l'a indiqué Noemi, la limite à droite en -1 n'existe pas.
Il y a la limite à gauche à chercher.
Dans un devoir, il faudrait bien sûr rédiger correctement.
$\underset{x\to (-1{)}^{-}}{\lim }1-x=1+1=2$
$\underset{x\to (-1{)}^{-}}{\lim }\sqrt{x^2-1}=0^{+}$
donc
$\underset{x\to (-1{)}^{-}}{\lim }f(x)=+\infty$

Tu peux bien sûr chercher aussi la limite (à droite) à 1, mais j'ai l'impression que ce n'est pas demandé dans ton exercice.

[mtschoon]

@Joyca-Le-Boss , je te mets quelques pistes pour la seconde limite à trouver.

Soit $g(x)=\frac{\sqrt{x^2-9}}{x^2-5x+6}$

Conditions d'existence :
$x^2-9\ge 0$ <=> $x\le -3$ ou $x\ge 3$
$x^2-5x+6\ne 0$ <=> $x\ne 2$ et $x\ne 3$
Tu dois trouver ( après avoir fait les calculs utiles)
$D=]-\infty ,-3]\cup ]3,+\infty [$

Donc , en 3, tu ne peux chercher que la limite à droite (la limite à gauche n'existe pas).

Il y a une indétermination du type $\frac{0}{0}$

Tu peux lever cette indétermination par factorisation du numérateur et dénominateur puis simplification.

Bons calculs.

[mtschoon]

f@Joyca-Le-Boss ,

Tu dois trouver $\underset{x\to 3^{+}}{\lim }g(x)=+\infty$

Reposte si besoin.