Calculs de limites de fonction avec une fraction et une racine carrée
-
Joyca Le Boss dernière édition par Noemi
Bonjour , Pouvez-vous m'aidez à résoudre ces 4 limites , svp ou me les corriger, merci d'avance pour votre aide !!!
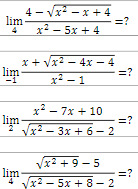
-
BBlack-Jack dernière édition par
On multiplie numérateur et dénominateur par (4 + V(x²-x+4))
(x²-5x+4) * (4 + V(x²-x+4)) = (x-1).(x-4).(4 + V(x²-x+4))
(4 - V(x²-x+4))(4 + V(x²-x+4))
= 16 - (x²-x+4)
= -x² + x + 12
= -(x-4)(x+3)---> lim(x-->4) (x-4)(x+3)/[(x-1)(x-4).(4 + V(x²-x+4))]
= lim(x-->4) (x+3)/[(x-1).(4 + V(x²-x+4))]
= (4+3)/[(4-1).(4 + V16)
= 7/(3 * 8 )
= 7/24
Essaie les autres, en t'aidant de la limite ci-dessus.
-
BBlack-Jack dernière édition par
Bonjour,
Pour la 2)
Multiplier numérateur et dénominateur par [x - V(x²-4x-4)]
...Pour la 3)
Multiplier numérateur et dénominateur par [V(x²-3x+6) + 4]
...Pour la 4)
Multiplier numérateur et dénominateur par [V(x²+9) + 5] * [V(x²-5x+8) + 2]
...Voila, il n'y a plus qu'à ...
-
mtschoon dernière édition par mtschoon

Bonjour,
@Joyca-Le-Boss , seulement une remarque sur l'énoncé.
Lorsqu'on travaille sur une fonction f, quelque soit la question, on commence par chercher l'ensemble de définition (pour savoir quelles valeurs on peut donner à x pour que f(x) existe).
C'est surprenant que ce ne soit pas demandé...peut-être que l'exercice est seulement "calculateur de limites".
Si c'est un devoir à rendre, je te conseille de chercher les ensembles de définition avant les limites (à toi de voir, bien sûr, ça allonge le travail !)
Par exemple, pour la première :
Conditions d'existence :
{x2−x+4≥0x2−5x+4≠0\begin{cases}x^2-x+4 \ge 0 \cr x^2-5x+4\ne 0\end{cases}{x2−x+4≥0x2−5x+4=0
Après calculs :
x2−x+4≥0x^2-x+4\ge 0x2−x+4≥0 : vrai pour tout x réel
x2−5x+4≠0x^2-5x+4\ne 0x2−5x+4=0 <=> x≠1x\ne 1x=1 et x≠4x\ne 4x=4D=R − D=R\ -\ \ D=R − {1,41,41,4}
Donc x peut tendre vers 4 par valeurs inférieures et par valeurs supérieures.
Bons calculs pour les limites et reposte si besoin.
-
mtschoon dernière édition par mtschoon

Bonjour,
Je regarde la première limite@Black-Jack a dit dans Pouvez-vous m'aidez à resoudre ces limites :
On multiplie numérateur et dénominateur par (4 + V(x²-x+4))
(x²-5x+4) * (4 + V(x²-x+4)) = (x-1).(x-4).(4 + V(x²-x+4))
(4 - V(x²-x+4))(4 + V(x²-x+4))
= 16 - (x²-x+4)
= -x² + x + 12
= -(x-4)(x+3)---> lim(x-->4) (x-4)(x+3)/[(x-1)(x-4).(4 + V(x²-x+4))]
= lim(x-->4) (x+3)/[(x-1).(4 + V(x²-x+4))]
= (4+3)/[(4-1).(4 + V16)
= 7/(3 * 8 )
= 7/24
Essaie les autres, en t'aidant de la limite ci-dessus.
Je vois une erreur de signe vers la fin du calcul .
Il manque un "-"Rectificatif :
En appelant f la fonction.
limx→4f(x)=limx→4−(x−4)(x+3)(x−1)(x−4)(4+x2−x+4)\displaystyle \lim_{x\to 4}f(x)=\lim_{x\to 4}\dfrac{-(x-4)(x+3)}{(x-1)(x-4)(4+\sqrt{x^2-x+4})}x→4limf(x)=x→4lim(x−1)(x−4)(4+x2−x+4)−(x−4)(x+3)
Après simplification par (x−4)(x-4)(x−4)
limx→4f(x)=limx→4−(x+3)(x−1)(4+x2−x+4)\displaystyle \lim_{x\to 4}f(x)=\lim_{x\to 4}\dfrac{-(x+3)}{(x-1)(4+\sqrt{x^2-x+4})}x→4limf(x)=x→4lim(x−1)(4+x2−x+4)−(x+3)
limx→4f(x)=−73×8=−724\displaystyle \lim_{x\to 4}f(x)=\dfrac{-7}{3\times 8}=\boxed{-\dfrac{7}{24}}x→4limf(x)=3×8−7=−247
-
BBlack-Jack dernière édition par
@mtschoon a dit dans Pouvez-vous m'aidez à resoudre ces limites :
(x²-5x+4) * (4 + V(x²-x+4)) = (x-1).(x-4).(4 + V(x²-x+4))
(4 - V(x²-x+4))(4 + V(x²-x+4))
= 16 - (x²-x+4)
= -x² + x + 12
= -(x-4)(x+3)
---> lim(x-->4) (x-4)(x+3)/[(x-1)(x-4).(4 + V(x²-x+4))]
= lim(x-->4) (x+3)/[(x-1).(4 + V(x²-x+4))]
= (4+3)/[(4-1).(4 + V16)
= 7/(3 * 8 )
= 7/24Erreur de signe ...
Yes, je suis contrit, enfin pas plus que cela devant le manque de réaction de l'aidé ... qui a un gros point noir à coté de son pseudo pour une aide future de ma part.
C'est à vous dégoûter d'intervenir pour aider des ingrats, de plus en plus présents sur les sites.(x²-5x+4) * (4 + V(x²-x+4)) = (x-1).(x-4).(4 + V(x²-x+4))
(4 - V(x²-x+4))(4 + V(x²-x+4))
= 16 - (x²-x+4)
= -x² + x + 12
= -(x-4)(x+3)---> lim(x-->4) -(x-4)(x+3)/[(x-1)(x-4).(4 + V(x²-x+4))]
= lim(x-->4) -(x+3)/[(x-1).(4 + V(x²-x+4))]
= -(4+3)/[(4-1).(4 + V16)
= -7/(3 * 8 )
= -7/24
-
mtschoon dernière édition par mtschoon

@Joyca-Le-Boss , je t'indique les limites que tu dois trouver aux trois dernières limites, sauf erreur :
à la deuxième : 111
à la troisième : −12-12−12
à la quatrième : 1615\dfrac{16}{15}1516Bons calculs.
Tiens noux au courant si problème.
-
Joyca Le Boss dernière édition par
@mtschoon voici mon raisonnement !
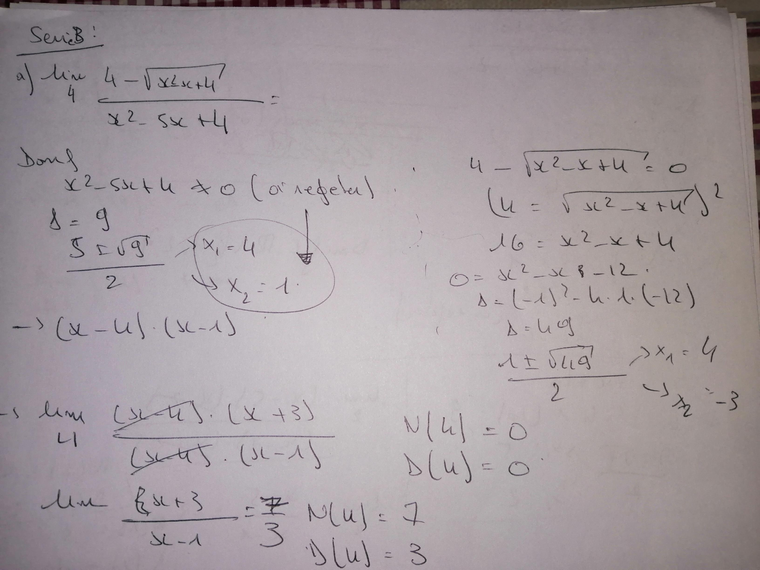
-
@Joyca-Le-Boss Bonsoir,
L'écriture de la fonction est fausse. Il faut multiplier numérateur et dénominateur par l'expression conjuguée du numérateur.
-
mtschoon dernière édition par mtschoon

Bonjour,
Pour la première limite, l'explication a été donnée dans les premières réponses. Tu peux les consulter.
Je regarde ton brouillon.
L'ensemble de définition est bon (il faut aussi s'assurer que x2−x+4x^2-x+4x2−x+4 est positif , ce qui est le cas).
Il y a une indétermination du type 00\dfrac{0}{0}00
Tu as bien compris qu'il faut factoriser numérateur et dénominateur par (x-4)
La factorisation de x2−5x+4x^2-5x+4x2−5x+4 est bonne.Comme te l'a indiqué Noemi, la transformation utile, en multipliant numérateur et dénominateur par l'expression conjuguée de 4−x2−x+44-\sqrt{x^2-x+4}4−x2−x+4, n'est pas bonne.
J'explicite un peu , en appelant f la fonction.
f(x)=(4−x2−x+4)(4+x2−x+4)(4+x2−x+4)(x2−5x+4)f(x)=\dfrac{(4-\sqrt{x^2-x+4})(4+\sqrt{x^2-x+4})}{(4+\sqrt{x^2-x+4})(x^2-5x+4)}f(x)=(4+x2−x+4)(x2−5x+4)(4−x2−x+4)(4+x2−x+4)
Tu développes le numérateur avec l'identité (a−b)(a+b)=a2−b2(a-b)(a+b)=a^2-b^2(a−b)(a+b)=a2−b2
Ce qui te donne :
f(x)=(16−(x2−x+4)(4+x2−x+4)(x2−5x+4)f(x)=\dfrac{(16-(x^2-x+4)}{(4+\sqrt{x^2-x+4})(x^2-5x+4)}f(x)=(4+x2−x+4)(x2−5x+4)(16−(x2−x+4)
f(x)=−x2+x+12(4+x2−x+4)(x2−5x+4)f(x)=\dfrac{-x^2+x+12}{(4+\sqrt{x^2-x+4})(x^2-5x+4)}f(x)=(4+x2−x+4)(x2−5x+4)−x2+x+12
En factorisant numérateur et dénominateur , tu obtiens
f(x)=−(x+3)(x−4)(4+x2−x+4)(x−1)(x−4)f(x)=\dfrac{-(x+3)(x-4)}{(4+\sqrt{x^2-x+4})(x-1)(x-4)}f(x)=(4+x2−x+4)(x−1)(x−4)−(x+3)(x−4)Il te reste à simplifer par (x-4) et déterminer la limite de l'expression simplifiée et tu trouveras −724-\dfrac{7}{24}−247
Refait tout ça correctement.
C'est cette méthode que tu dois utiliser pour les 3 autres limites.