Résolution d'une équation

Bonjour,
L'or d'un test de niveau on nous propose de résoudre l'équation x+ln(x)=0, pour moi j'ai passé par un changement de variable en posant que ln(x)=k pour tout k€Z et pour cela je retrouve x=exp(k) maintenant j'ai mon équation exp(k)+k=0 mais je suis bloqué de quelle valeur de k cette équation est nulle où faut il resté sur la même équation de départ pour résoudre ? Merci pour votre aide

@Simaths Bonjour,

Etudie la fonction $f (x) = x + l n (x)$
A partir des variations tu montres qu'il existe une valeur de $x$ qui annule $f (x)$ .

Tu cherches ensuite une valeur approchée.

@Noemi j'ai essayé cela en passant par la méthode de dichotomie mais je trouve seulement une continuité d'intervalle

@Simaths

Par dichotomie, tu dois trouvé pour $x$ , une valeur proche de 0,5671...

Bonjour,

@Simaths , suis la piste de Noemi en utilisant le théorème des valeurs intermédiaires
Ce théorème doit être dans ton cours
Il est détaillé ici ( regarde le pargraphe III, cas d'une fonction continue et strictement monotone).
https://www.parfenoff.org/pdf/Term_S/analyse/Term_S_Continuite_theor_val_interm.pdf

Soit $f (x) = x + l n (x)$
f est définie et dérivable (donc continue ) sur $]0,+∞[]0,+\infty[$
$f′(x)=1+1xf'(x)=1+\dfrac{1}{x}$
$f(x)>0f(x)\gt 0$ donc f strictement croissante.
Tu cherches les limites (faciles) en 0 (par valeurs positives) et en $+∞+\infty$
Tu peux faire le tableau de variations pour que ça soit plus clair.

Conclusion :
f est définie, continue, et strictement croissante de $]0,+∞[]0,+\infty[$ vers $]−∞,+∞[]-\infty,+\infty[$
$0∈]−∞,+∞[0\in]- \infty,+\infty[$
Avec le T.V.I., tu déduis qu'il y a une (et une seule) valeur $α\alpha$ de $]0,+∞[]0,+\infty[$ telle de $f (x) = 0$

L'équation $x + l n (x) = 0$ a donc pour solution $α\alpha$

A la calculette (ou autre) tu trouves une valeur approchée de $α\alpha$
Ma calculette me donne $α≈0.56\alpha \approx 0.56$

@Noemi , bonjour,

Quand j'ai commencé à écrire ma "prose", tu n'étais pas connectée...

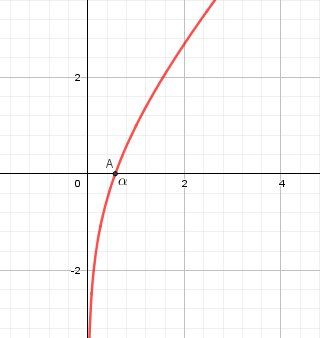
Illustration graphique
La représentation graphique de f est en rouge
A est le point d'intersection de la représentation graphique de f avec l'axe des abscisses, de coordonnées $(α,0)(\alpha,0)$

Bonjour,

Beaucoup a été dit, mais soit :

x + ln(x) = 0

On peut trouver la valeur de x en utilisant la fonction spéciale W de Lambert.
Cette fonction n'étant pas connue en Terminale, on peut alors approcher la valeur de x en étudiant les variations de f(x) = x + ln(x)

f(x) = x + ln(x)
Df : x > 0
f'(x) = 1 + 1/x = (x+1)/x

f'(x) > 0 sur R*+ --> f est strictement croissante.

f(1/e) = 1/e - 1 = -0,63... < 0
f(1) = 1 > 0

Des 3 lignes précédentes et par le théorème des valeurs intermédiaires, on peut dire qu'il y une et seule valeur alpha de x pour laquelle f(x) = 0 et

que alpha est comprise dans ]1/e ; 1[

On peut donc approcher alpha avec la précision qu'on veut (sauf valeur exacte) par une méthode dichotomique.
...

Remarque,

A partir du moment où il n'y a pas de balises dans l'énoncé sur la méthode à utiliser pour résoudre l'équation ... et que de toutes manières on ne peut pas trouver la valeur exacte de alpha, on pourrait tout aussi bien tracer la courbe représentant f(x) = x + ln(x) sur une calculette graphique ...
et y lire une valeur approchée de alpha. (pour f(x) = 0)

Ce serait probablement pénalisé par le prof, bien que cette méthode en vaut bien une autre.

Pour les curieux,

Tout à fait hors sujet en TS, mais puisque la fontion de Lambert est citée, voici un lien sur la constante $Ω\Omega$
qui répond à la question.
$α=Ω=W0(1)=0,56714329040978387299996866221035…\alpha = \Omega=W_0(1)=0,56714329040978387299996866221035 …$

http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaConst/Omega.htm