Trigonométrie / terminale S

Bonjour , mon exercice est un Vrai ou faux et il faut justifier ses réponses. L’énoncé est : soit f la fonction définie sur R par f(x) = 2 sin x + √2 x
1 . La fonction est impaire
Ma réponse est : Faux , la fonction racine carré n’est définie que sur R+ donc elle est ni paire ni impaire .
2. La fonction f est périodique de période 2pi
Ma réponse est : étudions la périodicité de la fonction f sur R : f(x) = 2 sin x + √2 x
= 2 sin (x+ 2pi) + √2(x+2pi)
= 2 sin x + √2(x+2pi)
# f(x)
Alors Faux .
3. La fonction f est croissante sur [ -3pi/4;3pi/4]
Ma réponse est : Faux car la fonction racine carré est seulement définie sur [ 0 ; + l’infini[
4. La fonction f est concave [pi;2pi]
Ma réponse est : Vrai car la fonction est concave sur [0, + l’infini[ et concave alors sur [pi;2pi]
5.La limite de f en + l’infini est est égale à + l’infini . Ma réponse est : Faux car la fonction f est définie sur [0;2pi] alors lim (x) (en + l’infini) =2pi
6. La limite de f(x)/x en + l’infini est égale à √2
Ma réponse : ici je n’ai pas réussie à trouver ..
J’aimerai savoir si mes réponses sont correctes et si mes justifications sont suffisantes . Merci de votre aide .

@jadedslv , bonjour,

Tu as dû faire cet exercice un peu rapidement car il y a des erreurs nombreuses

Tu as écrit : $f(x)=2sinx+2xf(x)=2sinx+\sqrt 2 x$

Il n'y a pas de fonction"racine carrée"

$2x\sqrt 2x$ veut dire $2×x\sqrt 2 \times x$

L'ensemble de défintion f est $R$

1 ) Etudie la parité ou l'imparité

2 )OK pour ta réponse, mais tu peux expliciter un peu plus pour trouver
$f(x+2π)=f(x)+22πf(x+2\pi)=f(x)+2\sqrt2\pi$

3 ) Calcule $f^{'} (x)$ et son signe sur l'intervalle donné

4 ) Calcule $f^{''} (x)$ et son signe sur l'intervalle donné

5 ) Lorsque x tend vers + $∞\infty$ , $s i n x$ est bornée entre -1 et +1, et x tend vers + $∞\infty$
Tu tires la conclusion

6 ) $lim⁡x→+∞f(x)x=lim⁡x→+∞2sinxx+2\displaystyle \lim_{x\to +\infty}\dfrac{f(x)}{x}=\lim_{x\to +\infty}2\dfrac{sinx}{x}+\sqrt2$
Tu tires la conclusion.

En bref, à part la question2), il faut que tu revois tes réponses.

Bon travail.

Je vous remercie , j’ai retravaillée mes questions :

F(x) = √2x+ 2sin(x)
Et f’(x)= 2cos(x)+ √2
Pour xE[-3pi/4;3pi/4] on a :
-3pi/4<x<3pi/4
-3pi/4 * 2cos(x) < 2cos(x) < 3pi/4 * 2cos(x)
-3pi/4 * 2cos(x)+ √2< 2cos(x)+ √2< 3pi/4 * 2cos(x)+ √2
Alors 0 < f’(x) et j’ai ensuite déduis le tableau de variation .

4.F’’(x) = -2sin(x)
Et f’’(x) est croissante d’après le tableau de variation que j’ai déduis sur l’intervalle alors elle est concave sur [ 0 , 2pi].

Je n’ai pas réussi à expliquer ..

Et pour la question 1 j’ai trouvé que la fonction était impaire car f(-x) = √2*-x+2sin(-x)
# f(x)

@jadedslv Bonsoir,

Une fonction est impaire si :
$x$ et $- x$ appartiennent au domaine de définition et si
$f (- x) = - f (x)$

Vérifie

Je trouve que f(-x) = -f(x) .. en simplifiant ce que j’avais trouvé

@jadedslv

Donc la fonction est impaire.

@jadedslv ,

Pour la question 1, Oui, f est impaire , car pour tout $x$ réel, $- x$ est réel et $f (- x) = - f (x)$

Pour la question 3) que tu as appelé 1) dans ton post précédent.
Oui, f est croissante.

Ta dérivée est bonne $f′(x)=2cosx+2f'(x)=2cosx+\sqrt 2$ et elle est positive donc f croissante.

Pour le justifier, tes encadrements sont à revoir.
Fais le cercle trigonométrique pour mieux comprendre et pense aux angles remarquables.

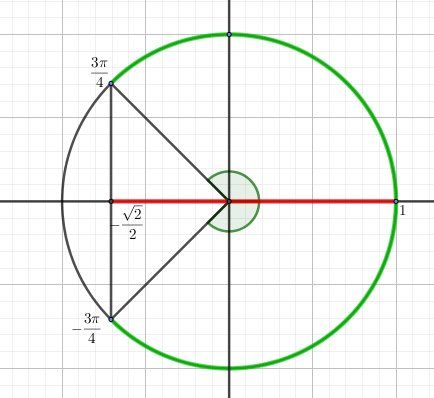
$−3π4≤x≤+3π4-\dfrac{3\pi}{4}\le x\le +\dfrac{3\pi}{4}$

$\ge -\dfrac{\sqrt 2}{2}$

$2cos(x)≥−22cos(x)\ge -\sqrt 2$

$2cos(x)+2≥02cos(x)+\sqrt 2\ge 0$

donc $\ge 0$

@jadedslv ,

Pour la question 4)

$f^{''} (x)$ est exacte mais c'est le signe de $f^{''} (x)$ que tu dois trouver.
(regarde ton cours sur les fonctions convexes et concaves)

Ici , tu dois trouver que $f^{''} (x)$ est positive donc f convexe.

Pour la question 5), relis ma piste d'explication.

Lorsque x tend vers $+∞+\infty$ , $2x\sqrt 2x$ tend vers $+∞+\infty$
En ajoutant $s i n x$ qui est compris entre -1 et +1, la somme des deux tend vers ....................
(je te laisse trouver)

Pour la question 6), relis ma piste d'explication.

sinx en compris entre -1 et +1.
En le divisant par x qui tend vers $+∞+\infty$ , le quotient $sinxx\dfrac{sinx}{x}$ tend vers .............................
(je te laisse trouver)

Tu auras ensuite la limite de $f (x)$

Pour la question 5 j’ai alors trouvé que f(x) tend vers + l’infini .
Pour la question 6 , j’ai alors trouvé que f(x) tend vers √2.
Est ce correct ?

@jadedslv ,

Oui c'est bon pour la 5) et la 6)

Je vous remercie énormément encore une fois !!!! Très bonne soirée à vous

De rien @jadedslv , tu as bien travaillé !
Revois tout ça de près.

Très bonne soirée à toi aussi et bonne semaine .

@jadedslv , bonjour,

Une remarque "hors sujet".

En consultant la rubrique « Terminale » je viens de m’apercevoir que tu a supprimé ton topic (posté 2 ou 3 jours avant celui-ci), relatif aux lois de probabilité ( calculs sur un cheptel de vaches laitières en période hivernale).
(C'est forcément toi qui a fait la suppression, car, à par le demandeur, seule la modération peut le faire).
Vu que le paramétrage du forum te le permet , tu en as le droit, mais ce n’est guère convivial...

On peut comprendre qu’un demandeur non satisfait le fasse, mais ce ne me semble être le cas ici.
Tu as terminé la discussion en précisant que "tu as tout compris" (et je m’en réjouis !).
Alors, pourquoi supprimer cette discussion constructive ?

Le forum est « public ». Les consultants y sont nombreux.
Ils peuvent travailler sur les questions/réponses pour s’entraîner et progresser. C’est ça l’entre-aide.
C’est l’esprit du forum (c’est pour cela que j’y participe).
Si chacun supprimait ses topics après avoir obtenu de l’aide, ce forum public n’aurait guère de sens...

Ce serait bien que tu réfléchisses à cet aspect des choses.

Bonne journée et bon travail.