Trouver l'equation d'une parabole a partir de deux ou trois points
-
Jérémie Obsomer dernière édition par
Bonjour, je n'arrive pas à trouver comment calculer l’équation d'une fonction à partir de deux ou trois points (du dessin en fait, mais je n'ai pris que les coordonnées de points ne contenant pas de décimale).
-
Jérémie Obsomer dernière édition par
J'ai, comme coordonnées, le sommet, et les ordonnées a l'origine, soit les intersections entre la parabole et l'axe des x. Pourriez-vous, s'il vous plait m'aider ?
Bien à vous et au plaisir de pouvoir lire vos réponses
-
mtschoon dernière édition par mtschoon

@Jérémie-Obsomer , bonjour,
Tu postes en 3ème, mais ta question est plutôt de niveau Seconde...
Je te mets un lien pour l'équation d'une parabole (f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c avec a≠0a\ne 0a=0) connaissant les coordonnées du sommet et d'un point.
https://www.youtube.com/watch?v=XynjWEEXZp8
Regarde cela de près et reposte si besoin.
Si tu as un exercice, écris ton énoncé exact et tu pourras avoir des détails précis.
-
mtschoon dernière édition par mtschoon

@Jérémie-Obsomer , re-bonjour,
Je te mets un exemple, en utilisant les mêmes notations que sur la vidéo proposée, et qui semble convenir à ce que tu cherches :
Parabole dont on connait le sommet S(2,1) et un des points d'insersection B(1,0) de la parabole avec l'axe des abscisses ( un point d'intersection avec l'axe des abscisses suffit pour le calcul)forme développée : f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c
forme canonique : f(x)=a(x−α)2+βf(x)=a(x-\alpha)^2+\betaf(x)=a(x−α)2+β
(α,β)(\alpha,\beta)(α,β) sont ls coordonnées de S, donc :
f(x)=a(x−2)2+1f(x)=a(x-2)^2+1f(x)=a(x−2)2+1La parabole passe par le point B(1,0), donc pour x=1x=1x=1, f(x)=0f(x)=0f(x)=0 :
0=a(1−2)2+10=a(1-2)^2+10=a(1−2)2+1 <=>0=a(−1)2+10=a(-1)^2+10=a(−1)2+1 <=> 0=a+10=a+10=a+1
Au final , a=−1a=-1a=−1La forme canonique est donc :
f(x)=−1(x−2)2+1f(x)=-1(x-2)^2+1f(x)=−1(x−2)2+1, c'est à dire : f(x)=−(x−2)2+1\boxed{f(x)=-(x-2)^2+1}f(x)=−(x−2)2+1Si l'on veut la forme développée :
f(x)−(x2−4x+4)−1f(x)-(x^2-4x+4)-1f(x)−(x2−4x+4)−1
f(x)=−x2+4x−4+1f(x)=-x^2+4x-4+1f(x)=−x2+4x−4+1
f(x)=−x2+4x−3\boxed{f(x)=-x^2+4x-3}f(x)=−x2+4x−3
-
mtschoon dernière édition par

Illustration graphique :
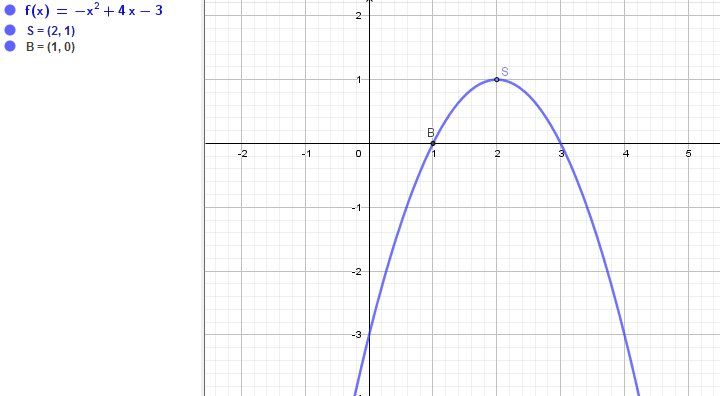
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
S'il s'agit de paraboles (comme dans le titre du topic) ...
Trop souvent en Secondaire ... les énoncés sont scabreux.
Si on ne précise pas l'orientation de l'axe de la parabole par rapport aux axes du repère, une parabole n'est pas définie par 3 points.
Par exemple les 3 paraboles dont les équations suivent :
3x² + 6xy + 3y² - 5x - 7y = 0 (axe oblique par rapport aux axes du repère)
3x² - 5x - 2y = 0 (axe parallèle à l'axe des ordonnées)
3y² - y - 2x = 0 (axe parallèle à l'axe des abscisses)
... passent toutes par les points de coordonnées (0;0) et (1;1) et (2;-1)
Même si au Secondaire, on se limite souvent aux paraboles avec axe parallèle à l'axe des ordonnées ... on ne peut pas ignorer les autres cas dans un énoncé.
L'énoncé DOIT préciser la direction de l'axe dans un tel énoncé.
... sauf, bien entendu, si l'énoncé fournit explicitement la forme de l'équation (par exemple y = ax² + bx + c) et 3 informations (par exemple 3 points de la parabole).
-
Jérémie Obsomer dernière édition par Jérémie Obsomer
@mtschoon
Bonjour, avant tout, merci de vos réponses, je pense avoir compris maintenant.
Mais, pour être sûre, je n'ai pas nécessairement besoin d'un point situé sur l'axe des X, si ?
Pour info, je suis en 4ᵉ, mais dans le système scolaire belge, je ne sais donc pas vraiment a quoi cela correspond.
En tout cas, je vais alors allez poser le reste de mes interrogations dans le forum de seconde.
Merci beaucoup de votre aide, elle m'as été très utile.
Bien à vous
-
mtschoon dernière édition par

@Jérémie-Obsomer , de rien .
Non, comme tu l'as vu dans la vidéo proposée, le point supplémentaire (en plus du sommet) n'est pas forcément sur l'axe des abscisses.
Effectivement, les rubriques de ce forum sont prévues pour le système français ...
Il faudrait connaître les équivalences avec le système belge...C'est effectivement préférable que tu donnes tes questions en lycée (à partir de la Seconde).
-
BBlack-Jack dernière édition par
Pour info
Belgique : 6ème primaire ; France : 6ème secondaire
Belgique : 1ère Secondaire ; France : 5ème secondaire
Belgique : 2ème Secondaire ; France : 4ème secondaire
Belgique : 3ème Secondaire ; France : 3ème secondaire
Belgique : 4ème Secondaire ; France : Seconde
Belgique : 5ème Secondaire ; France : Première
Belgique : 6ème Secondaire ; France : Terminale
-
mtschoon dernière édition par

Bonsoir,
Merci pour l'info.
Donc, tout est OK
@Jérémie-Obsomer qui est en 4ème(Belgique) doit bien poster ici en Seconde (France).
-
Jérémie Obsomer dernière édition par
@Black-Jack
Merci pour l'info
Bien à toi
-
mtschoon dernière édition par

@Jérémie-Obsomer , une précision pour le forum.
@Jérémie-Obsomer a dit dans Trouver l'equation d'une parabole a partir de deux ou trois points :
Bonjour, je n'arrive pas à trouver comment calculer l’équation d'une fonction à partir de deux ou trois points (du dessin en fait, mais je n'ai pris que les coordonnées de points ne contenant pas de décimale).
Sur ce forum, les énoncés des exercices doivent être tapés au clavier (non scannés).
Par contre, les scans de dessins, images, tableaux numériques sont autorisés.Donc, pour cet exercice, si tu as besoin d'une aide précise, tu peux scanner le dessin que l'énoncé te donne, pour éviter d'être dans le flou...
-
Jérémie Obsomer dernière édition par
@mtschoon merci, mais ce sont des exercices que je dois effectuer à partir du site Oscar,
ci-dessous, les réponses que j'ai trouvées (sont-elles justes ?)
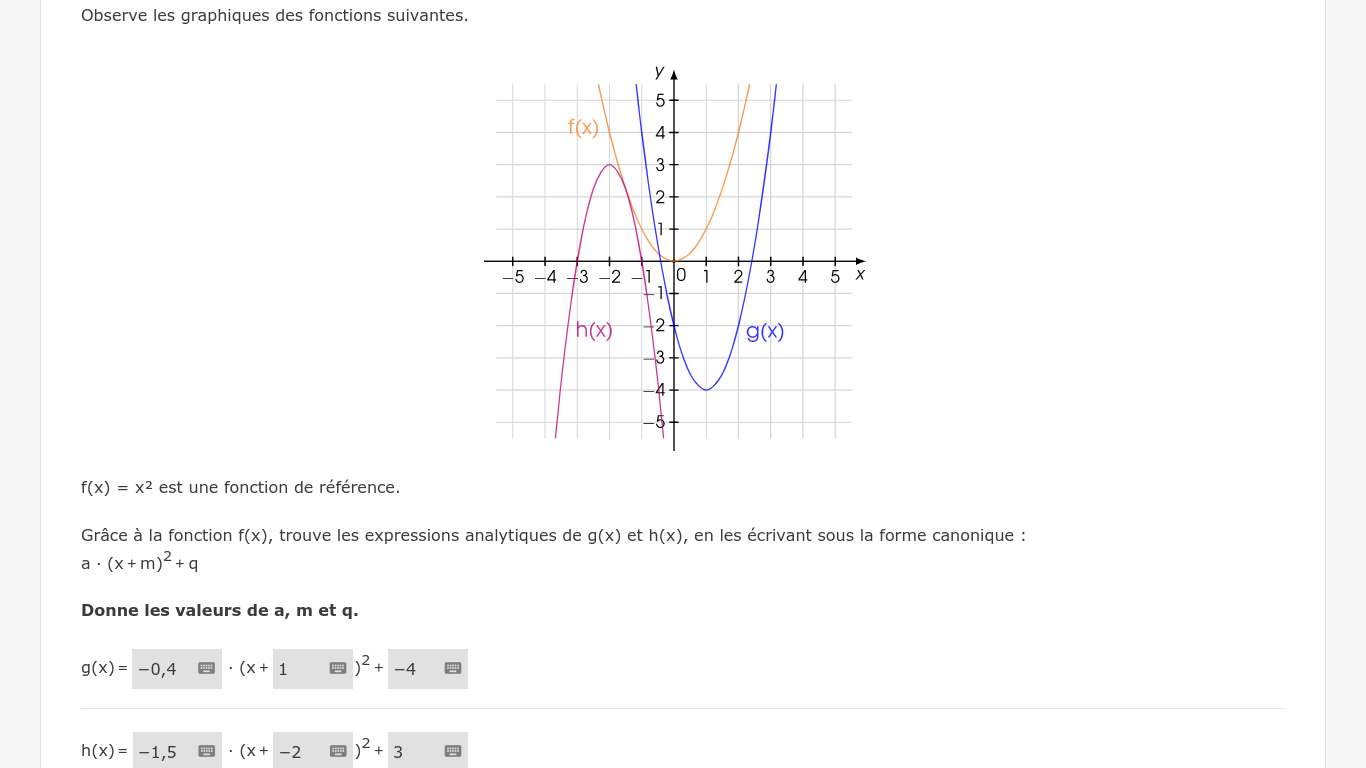
capture d'écran de la Série d'exercices n°1728 effectué à partir du site Oscar
merci beaucoup de votre aide pour cet exercice @mtschoon @Black-Jack
-
Jérémie Obsomer dernière édition par
@mtschoon mais, comme vous dites, lorsque je souhaite vous montrer mes exercices, je ne peux capture que le dessin, et pas les mots ?
-
@Jérémie-Obsomer Bonjour,
Oui, tu dois écrire l'énoncé de l'exercice et indiquer la question qui te pose problème.
Pour les scans, seuls sont autorisés, les graphiques, schémas ou figures.
-
Jérémie Obsomer dernière édition par
@Noemi Merci de l'information, je ferais plus attention a l'avenir
-
mtschoon dernière édition par mtschoon

Bonjour,
@Jérémie-Obsomer , c'est tout-à-fait ça pour le fonctionnement du forum.
Comme déjà dit, l'énoncé (le texte , c'est-à-dire "les mots") doivent être écrits (en tapant au clavier), mais tu peux scanner figures, graphiques. pour éclairer la compréhension de l'exercice.
-
Pour un nouveau exercice, il faut créer un autre sujet.
Dans les réponses données, le aaaet le mmm sont à rectifier.
-
mtschoon dernière édition par mtschoon

Re-bonjour,
@Jérémie-Obsomer , à regarder de près, je pense, sauf erreur de ma part, que le graphique que tu viens de mettre est relatif à la question de ce topic et c'est celui que tu aurais dû donner au début de ce topic.
Si c'est bien ça, tu n'avais pas de raison d'ouvrir une autre discussion.
Je regarde g(x) en utilisant l'explication donnée précédemment.
Soit S(α,β)S(\alpha,\beta)S(α,β) le sommet de la parabole
g(x)=a(x−α)2+βg(x)=a(x-\alpha)^2+\betag(x)=a(x−α)2+βPour g, S(1,−4)S(1,-4)S(1,−4)donc g(x)=a(x−1)2−4g(x)=a(x-1)^2-4g(x)=a(x−1)2−4
Pour trouver la valeur de a, tu prends un point simple , par exemple (0,−2)(0,-2)(0,−2) ou (2,−2)(2,-2)(2,−2)Avec (0−2)(0-2)(0−2) :
g(0)=−2g(0)=-2g(0)=−2 <=> a(−1)2−4=−2a(-1)^2-4=-2a(−1)2−4=−2 <=> a−4=−2a-4=-2a−4=−2 <=> a=2a=2a=2Donc g(x)=2(x−1)2−4\boxed{g(x)=2(x-1)^2-4}g(x)=2(x−1)2−4
Tu peux donner ta nouvelle réponse pour h(x) (vu que ta première est inexacte) si tu souhaites une vérification.
-
Jérémie Obsomer dernière édition par
@mtschoon pourquoi indique tu dans les parenthèse x moins alpha? et non pas x plus alpha?
-
mtschoon dernière édition par

Comme déjà indiqué, j'ai utilisé la propriété relative à la forme canonique avec les notations utilisées depuis le début de la discussion (voir, par exemple, la vidéo jointe).
Soit S(α,β)S(\alpha, \beta)S(α,β) sommet de la parabole .
f(x)=a(x−α)2+β\boxed{f(x)=a(x-\alpha)^2+\beta}f(x)=a(x−α)2+βEn identifiant avec les notations de ta fiche :
−α=+m\boxed{-\alpha=+m}−α=+m et β=q\boxed{\beta=q}β=q