Limite de la fonction rationnelle avec valeur absolue

Bonjour j'ai un petit problème à calculer la limite de f(x)=x^2 - x/ |1-x| quand x tend vers + l'infini , et merci d'avance

@ABCD-EFGH et avec plus de précision, je veux juste plus d'explication pour comment faire avec |1-x| et si ça dépend de x , autrement dit , |1-x|=1-x si x<1 et x-1 si x>1 . Alors on a pour la limite x tend vers + l'infini, donc je me demande si c'est la raison de choisir x-1 et non pas 1-x car pour x-1 ; x>1 et comme cela +l'infini est aux bornes de x . Et merci d'avance.

@ABCD-EFGH Bonjour,

C'est bien $x - 1$ qui correspond à la valeur absolue, donc la limite est bien $+∞+\infty$ , si la fonction est bien : $f(x)=x2−x∣1−x∣f(x)=\dfrac{x^2-x}{\vert1-x\vert}$ .

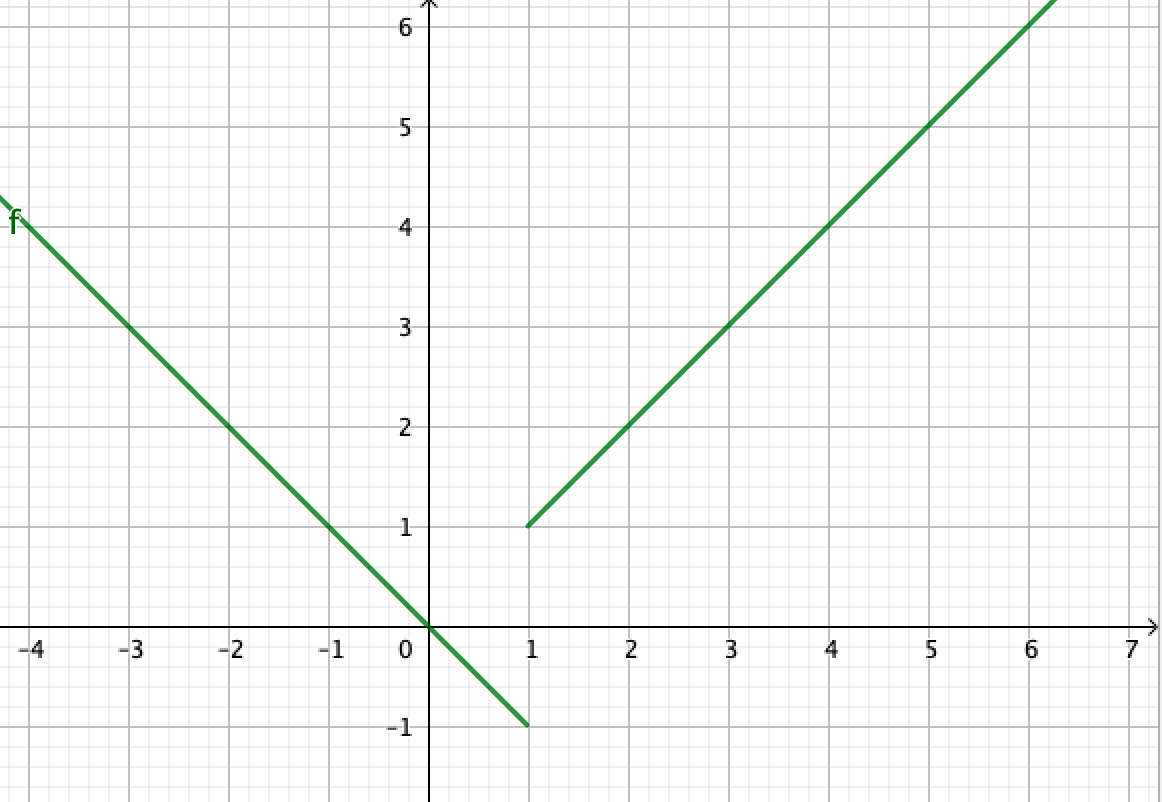
La représentation graphique pour vérifier les limites.

@Noemi merci beaucoup , or sans représentation graphique, est ce qu'il faut choisir pour la valeur absolue la solution dans laquelle +l'infini est aux bornes de x ;( x-1 / x>1 ), comme dans cet exemple où on doit calculer la limite en +l'infini ?

@ABCD-EFGH

Oui, ton raisonnement est correct.

La représentation graphique te permet juste une vérification.

@Noemi d'accord merci infiniment

Ce message a été supprimé !