Devoir maison de mathématique S

[Lola Clvd]

Sujet de devoir maison: J’aurais vraiment besoin d’aide

On considère deux suites (an) et (bn) définies par a0=1 et b0= 0 et pour tout entier naturel n.
an+1= √2an-bn
bn+1= an+ √2bn

(le n est en réalité plus bas que la lettre d’avant avec le +1)

1. Calculer a1, a2 et b1, b2
2. on souhaite écrire un algorithme qui affiche en sortie les valeurs de aN et bN pour une valeur entière de IN saisie par l’utilisateur. on propose l’algorithme suivant :

A <— 1
B <— 0
Pour K variant de 1 à N
A <— √2 A - B
B <— A + √2B
Fin pour

a) on choisit N= 2
Qu’elles valeurs numériques contiennent les variables A et B a la fin de l’exécution de l’algorithme ?
b) Ces résultats sont-ils cohérents avec ceux obtenues à la question 1 ? Dans le cas contraire, écrire une version corrigée de l’algorithme pour qu’il affiche les résultats souhaités (on pourra utiliser une troisième variable, notée C)

[Noemi]

@Lola-Clvd Bonsoir,

Question 1
Si $n=0$,
$a_1=\sqrt{2}{a}_0-b_0$, soit $a_1=\sqrt{2}\times 1-0=\sqrt{2}$
$b_1=a_0+\sqrt{2}{b}_0$, soit $b_1=1+\sqrt{2}\times 0=1$
Si $n=1$
$a_2=\sqrt{2}{a}_1-b_1$, soit $a_2=\sqrt{2}\times \sqrt{2}-1=2-1=1$

Applique le même raisonnement pour le calcul de $b_2$.
Question 2
Pour $K=1$
$A=\sqrt{2}\times 1-0=\sqrt{2}$
$B=\sqrt{2}+\sqrt{2}\times 0=\sqrt{2}$

Exécute le programme pour $K=2$. soit une autre boucle.

Indique tes réponses si tu souhaites une vérification.

[mtschoon]

Bonjour,

Complément éventuel,

Après les valeurs déjà calculées,
$b_2=a_1+\sqrt{2}{b}_1=\sqrt{2}+\sqrt{2}=2\sqrt{2}$,
Puis, en continuant , on trouve $a_3=-\sqrt{2}$ , $b_3=5$

Effectivement, l'algorithme donné doit être modifié.
Après $A\leftarrow \sqrt{2}A-B$, le calcul de B à la ligne suivante est fait avec la nouvelle valeur de A (c'est à dire $\sqrt{2}A-B$) au lieu de l'ancienne.

Utilisation de la variable C pour palier à cette erreur :

Algorithme ainsi modifié écrit sous forme "naturelle"avec Algobox, après avoir déclaré les variables A,B,N,K,C (nombres)

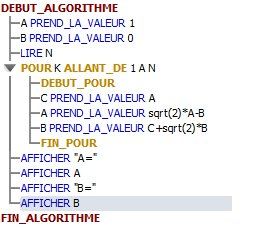
Test fait avec Algobox, pour N=3