Exercice suite géométrique

Bonjour je bloque beaucoup sur cette exercice est ce quelqu’un pourrait m’aider s’il vous plais ?!
On sait que a, b et c sont trois termes positifs et consécutifs d'une suite géométrique
croissante vérifiant le système:
a+b+c =39
abc = 1000
Déterminer a , b et c.
Voilà ce que j’ai fais !

@menel Bonjour,

De $b^3= 1000$ , tu en déduis $b = . . .$
A partir de $b+bq+bq2q=39\dfrac{b+bq+bq^2}{q}=39$
tu déduis $b+bq+bq^2=39q$
Equation à résoudre en remplaçant $b$ par la valeur trouvée.

Puis tu cherche $a$ et $c$ .

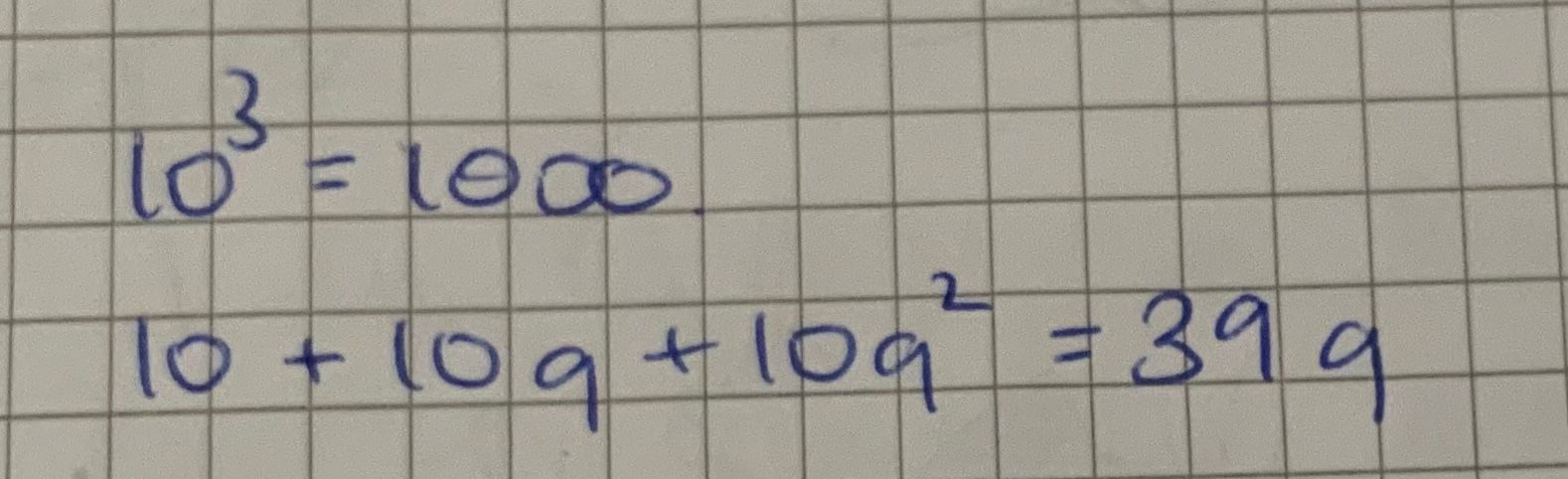
Comme cela ?

@Noemi je vois pas comment les trouver? delta ?

@menel

Pour déterminer la raison, tu peux utiliser la méthode avec delta.
Simplifie d'abord l'équation.
$10q^2-29q+10=0$

Tu dois trouver deux valeurs pour la raison : 0,4 et 2,5.
Détermine les termes sachant que la suite est croissante.

@Noemi delta m’a donner 441 et x1=-2,5 et x2=-0,4
Je me suis trompé non ??
Pourtant j’ai refais mes calcul deux fois

@menel

une erreur de signe
Les solutions :
$x1=−b−Δ2ax_1=\dfrac{-b-\sqrt{\Delta}}{2a}$

$x1=29−2120=0,4x_1=\dfrac{29-21}{20}=0,4$

$x2=−b+Δ2ax_2=\dfrac{-b+\sqrt{\Delta}}{2a}$

$x2=29+2120=2,5x_2=\dfrac{29+21}{20}=2,5$

Merci bcp pour votre aide