Calcul de limite difficile

Bonjour tous le monde
J’arrive pas à résoudre cette limite
( [(2-x^2).sin(x)]-[sin(2x)] )/ x^5
Quand x tend vers 0?
mais sans utiliser la règle de l’hopital
Svp je fais comment

@léna Bonjour,

Utilise les relations :
$s i n (2 x) = 2 s i n (x) c o s (x)$ puis tu factorises ;
$0sinxx=1\displaystyle \lim_{x\to\ 0} \dfrac{sinx}{x}=1$
tu utilises ensuite
$(1−cos(x))=2sin2x2(1-cos(x))=2sin^2\dfrac{x}{2}$

Indique tes calculs et/ou résultat si tu souhaites une vérification.

Bonjour,

Je reste perplexe...

Sauf erreur de ma part, utiliser simplement $(1−cos(x))=2sin2x2(1-cos(x))=2sin^2\dfrac{x}{2}$ amène à une indétermination...sauf en faisant peut-être d'autres transformations que je n'ai pas cherchées pour rester dans le programme de Terminale...

Par contre, prendre le développement limité de $(1 - c o s (x))$ d'ordre 4 au voisinage de 0, lève sans difficulté l'indétermination et aboutit à la limite $−112\boxed{-\dfrac{1}{12}}$

@léna , es-tu vraiment en Terminale ?
Je trouve que les limites que tu demandes sont difficiles pour des élèves qui commencent juste l'année scolaire...après une année de Première en pointillés...
Ou alors, tu es dans une "super-Terminale" ?

@Noemi
Bonsoir je m’excuse pour le retard j’avais cours alors j’ai essayer mais je n’ai pas pu la faire

@mtschoon
Bonsoir à vous je m'excuse pour le retard j’avais cours alors non je n’en suis pas en super terminal pas prof ma donner une série de limite pour m’exercer

Bonjour @léna ,

Je suis toujours aussi perplexe...de la pertinence de cet exercice en Terminale...

Evidemment , le début est très accessible.

Tu peux écrire
$f(x)=sinxx[−x2+2(1−cosx)x4]f(x)=\dfrac{sinx}{x}\biggr[\dfrac{-x^2+2(1-cosx)}{x^4}\biggr]$

Tu sais que $sinxx\dfrac{sinx}{x}$ tend vers 1 lorsque $x$ tend vers 0.

Soit $g(x)=−x2+2(1−cosx)x4g(x)=\dfrac{-x^2+2(1-cosx)}{x^4}$

Reste à lever l'indétermination du type $00\dfrac{0}{0}$ pour $g (x)$ , lorsque $x$ tend vers 0.

Si par chance (? ? ?) ton cours t'indique que, au voisinage de 0, $\approx 1-\dfrac{x^2}{2}+\dfrac{x^4}{24}$ , tu peux terminer sans difficulté et trouver la limite que je t'ai indiquée.

Sinon, c'est galère.

Bon entraînement...

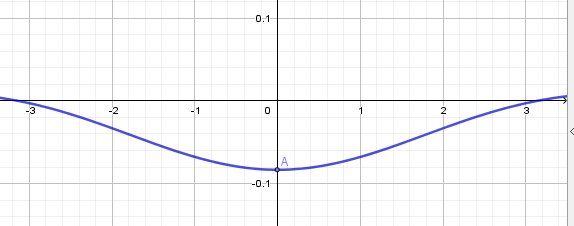
Représentation graphique de la fonction f au voisinage de 0

La point A (qui ne fait pas partie de la courbe) a pour ordonnée $−0.08333...=−112-0.08333...=-\dfrac{1}{12}$

@mtschoon
Bonjour alors j’ai essayer avec la formule que vous m’avez donner et j’ai pu la résoudre
Mais en effet ya pas cette formule dans mon cours

@léna, c'est très bien d'avoir réussi.

Effectivement, la formule que je t'ai indiquée (développement limité d'ordre 3) se traite normalement en Bac+1

Si tu as beaucoup de courage , tu peux essayer de lever l'indétermination en transformant avec le cosinus de l'angle moitié utilisée deux fois, ou autre ( je t'avoue ne pas avoir essayé) ou alors, tu attends la solution de ton professeur...