équation du second degré

Bonjour !

Dans l'exercice que je fais je dois étudier une fonction du second degré mais je bloque à la quetsion
en déduire suivant les valeurs du réel m le nombre de solution de l'équation f(x)=m
sauf que dans les questions d'avant il n'était pas question de m
pouvez vous me donner un indice sur comment résoudre cette question
Merci d'avance !

@Livindiam-Livin Bonjour,

A partir du tableau de variations de la fonction $f$ , tu dois étudier le nombre de points d'intersection de la courbe représentative de la fonction avec la droite $y = m$ .

@Livindiam-Livin , bonjour,

Il faut discuter suivant la valeur de m
Tu peux , pour éclairer ta question faire la représentation graphique de f (ou bien observer le tableau de variation).

Les solutions de l'équation f(x)=m sont les abscisses des points d'intersection de la parabole d'équation y=f(x) avec la droite (parallèle à l'axe des abscisses) d'équation y=m

Suivant les valeurs de m, tu trouveras 0 ou 1 ou 2 solutions.

@mtschoon sachant que la parabole est disjointe il y a 0 solution ?

@Livindiam-Livin ,

Effectivement si la droite d'équation $y = m$ ne rencontre pas la parabole, il y a 0 solution.

Si si la droite d'équation $y = m$ touche la parabole en 1 point (droite tangente à la parabole), il y a 1 solution.

Si si la droite d'équation $y = m$ coupe la parabole en 2 points , il y a 2 solutions.

@Livindiam-Livin , je te mets , pour plus de clarté, un exemple mais la fonction f que je prends n'est pas celle de ton énoncé (que l'on ne connait pas )

Soit $f(x)=2x^2+4x-3$
Le minimum est pour $x = - 1$ et il vaut $- 5$

Pour $m<−5m\lt -5$ la droite est en dessous de la parabole .
aucune solution à l'équation

Pour $m = - 5$ , la droite touche la parabole au point S(-1,-5)
une solution à l'équation (qui est x=-1)

Pour $m>−5m\gt -5$ , la droite coupe la parabole en deux points .
deux solutions qui sont les abscisses de ces deux points.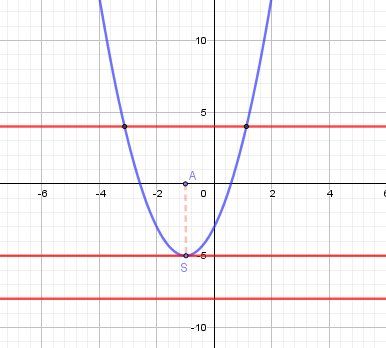

parmètre.jpg

Reposte si tu veux une vérification à tes réponses (mais pour cela il faut donner l'expression de f(x) de ton énoncé).

@mtschoon f(x)=-3x^2+6x-4 avec alpha qui vaut 1 et beta -1

dans mon énoncé on doit faire f(x)=m donc je pense qu'il y a 1 solution à savoir 1

@Livindiam-Livin ,

La parabole d'équation $f(x)=-3x^2+6x-4$ a sa concavité vers le bas.
Son sommet est effectivement le point S de coordonnées (1,-1)

Pour $\gt -1$ , la droite d'équation $y = m$ ne touche pas la parabole . Aucune solution à l'équation f(x)=m

Pour $m = - 1$ , la droite d'équation $y = m$ touche la parabole au point S. Une solution à l'équation f(x)=m (qui est x=1)

Pour $\lt -1$ , la droite d'équation $y = m$ coupe la parabole en deux points. Deux solutions à l'équation f(x)=m

@Livindiam-Livin ,

Schéma

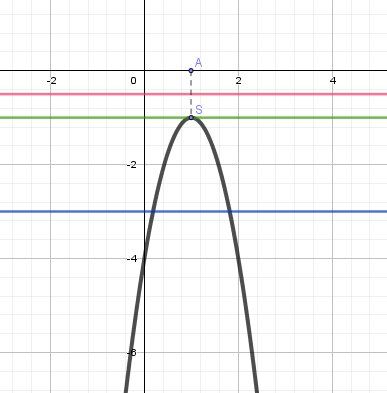
Le cas $m>−1m\gt -1$ est illustré par la droite en rouge
Le cas $m = - 1$ est illustré par la droite en vert
Le cas $m<−1m\lt -1$ est illustré par la droite en bleu

@mtschoon c'est comlpris, merci pour votre aide !

De rien @Livindiam-Livin .
C'est parfait si c'est clair pour toi.
Bonne semaine .