résoudre inéquation quotient

Bonjour !

je dois résoudre 2/x-3 - 3/x+2 >_ -1

J'ai commencée par faire en sorte que ce soit supérieur ou égale à 0 en fesant passer le -1 de l'autre coté soit
1+2/x-3 - 3/x+2 >_ 0

Que dois je faire ensuite pour mettre tout au même dénominateur?

Merci d'avance pour votre aide !

@Livindiam-Livin Bonjour,

Le dénominateur commun est $(x - 3) (x + 2)$ donc met chaque terme avec ce dénominateur commun:
$1$ devient $(x−3)(x+2)(x−3)(x+2)\dfrac{(x-3)(x+2)}{(x-3)(x+2)}$

Tu simplifies le numérateur puis tu étudies le signe de l'ensemble : numérateur et dénominateur

@Noemi d'accord merci pour votre aide !

@Livindiam-Livin

Indique tes calculs et/ou résultat si tu souhaites une vérification.

@Noemi donc je multiplie par (x−3)(x+2)(x-3) et ensuite je résultat est car 1+2-3=0 ou est ce que je dévellope le 2 et le 3 ?

@Livindiam-Livin

Non,

Tu multiplies le numérateur et le dénominateur de chaque terme afin que le dénominateur soit égal à $(x - 3) (x + 2)$
Exemple :
pour $2x−3\dfrac{2}{x-3}$ tu multiplies numérateur et dénominateur par $(x + 2)$
soit : $2x−3=2(x+2)(x−3)(x+2)\dfrac{2}{x-3}= \dfrac{2(x+2)}{(x-3)(x+2)}$

$1+2x−3−3x+2=(x−3)(x+2)(x−3)(x+2)+2(x+2)(x−3)(x+2)−3(x−3)(x−3)(x+2)1+\dfrac{2}{x-3}-\dfrac{3}{x+2}= \dfrac{(x-3)(x+2)}{(x-3)(x+2)}+\dfrac{2(x+2)}{(x-3)(x+2)}-\dfrac{3(x-3)}{(x-3)(x+2)}$
$=(x−3)(x+2)+2(x+2)−3(x−3)(x−3)(x+2)=....=\dfrac{(x-3)(x+2)+2(x+2)-3(x-3)}{(x-3)(x+2)}=....$

Développe et simplifie le numérateur.

@Noemi alors au numératuer il y a x^2-1x-6+2(x+2)-3(x--3)

@Livindiam-Livin

Développe et simplifie cette expression.

@Noemi alors au numérateur il y a x^2-2x+7

@Livindiam-Livin

C'est correct.

Cherche la forme canonique de ce polynôme.

@Noemi mais sachant que je dois étudier cette inéquation ne dois je pas chercher le discriminant ? car ensuite ej dois faire un tableau de signe

@Livindiam-Livin

Tu peux utiliser la méthode avec le discriminant.

Bonjour,

@Livindiam-Livin , quelques compléments si besoin.

Avant de résoudre l'inéquation, tu dois savoir sur quel ensemble de nombres tu travailles.
Ici, vu qu'il y a un quotient, tu dois imposer les conditions (dénominateur non nul) pour que le quotient existe.
$x−3≠0x-3\ne 0$ <=> $x≠3x\ne 3$
$x+2≠0x+2\ne 0$ <=> $x≠−2x\ne -2$
Tu cherches les solutions à cette inéquation sur $D = R$ /{-2,3}.
Si tu préfères, tu peux écrire : $D=]∞,−2[∪]−2,3[∪]3,+∞[D=]\infty,-2[\cup ]-2,3[\cup]3,+\infty[$
Cela doit être fait au début de l'exercice.

Lorsque tu feras le tableau de signes, il faudra mettre une double barre pour $x = - 2$ et $x = 3$ à la ligne relative au quotient .

Si j'ai bien lu, d'après les calculs faits, l'inéquation s'écrit
$x2−2x+7(x−3)(x+2)≥0\dfrac{x^2-2x+7}{(x-3)(x+2)}\ge 0$

le numérateur est un polynôme du second degré.
Son discriminant est strictement négatif (tu dois trouver $Δ=−24\Delta=-24$ )
Regarde ton cours :
Dans ce cas, le polynôme est toujours du signe de a (coefficient de $x^2$ )
Ici a=1 donc $x^2-2x+7$ est strictement positif pour tout x réel.

Il te reste à faire le tableau des signes et tirer la conclusion.

Tu peux donner ta réponse si tu souhaites une vérification.

@Livindiam-Livin ,

Si tu as besoin d'un rappel sur le signe d'un polynôme du second degré, tu peux regarder ici paragraphe II

https://www.mathforu.com/premiere-s/le-second-degre-2eme-partie/

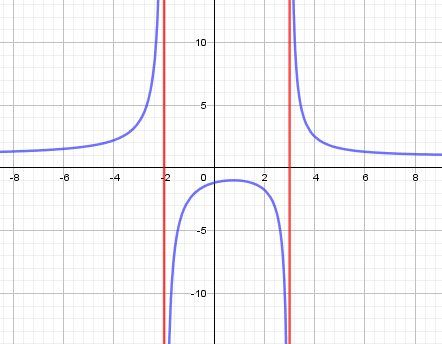
@Livindiam-Livin , pour pouvoir vérifier ton tableau de signes, tu peux faire la représentation garphique de f définie par $f(x)=x2−2x+7(x−3)(x+2)f(x)=\dfrac{x^2-2x+7}{(x-3)(x+2)}$ sur ta calculette et observer le signe de f(x) (au dessus ou au dessous de l'axe des abscisses)

Remarque ; la représentation graphique de f est en bleu
Les deux droites en rouge (d'équation x=3 et x=-2) ne font pas partie de la représentation grahique de f ; elles correspondent aus deux valeurs "interdites".
Si tu connais, elles sont asymptôtes à la représentation de f.