exo sur le quatrième degrés première

Bonjour, je n'arrive pas à faire cet exercice, je n'ai pas encore appris à résoudre les équations du quatrième degrés...

Une équation de degré quatre
P est la fonction définie sur R par :
P(x)= -2x^4 + 5x^3+14x^2-5x-12

a. Calculer
Déterminer les valeurs des nombres réels
a,b et c tels que, tout nombre x appartient au réel, p(x)= (x^2-1)(ax^2+bx+c)

b. Résoudre dans R l’équation P(x) = 0.
Comparer l’ensemble solution obtenu avec celui affiché par le logiciel de calcul formel :
Voir pièce jointe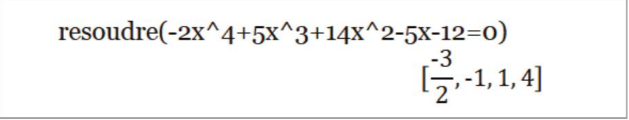

c. En déduire une factorisation de P(x), puis résoudre dans R l’inéquation P(x) ≤ 0.

@Julie243554 , bonjour,

La méthode par identification est expliquée ici.

Consulte là et donne tes réponses si tu veux une vérification.

https://www.mathforu.com/premiere-s/factorisation-d-un-polynome-par-identification/

merci beaucoup, j'en suis au c mais je ne sais pas si mon tableau de signe est juste, pourriez vous verifier si je peux vous l'envoyer en photo ?

@Julie243554 Bonjour,

Tu peux transmettre une photo du tableau de signes.

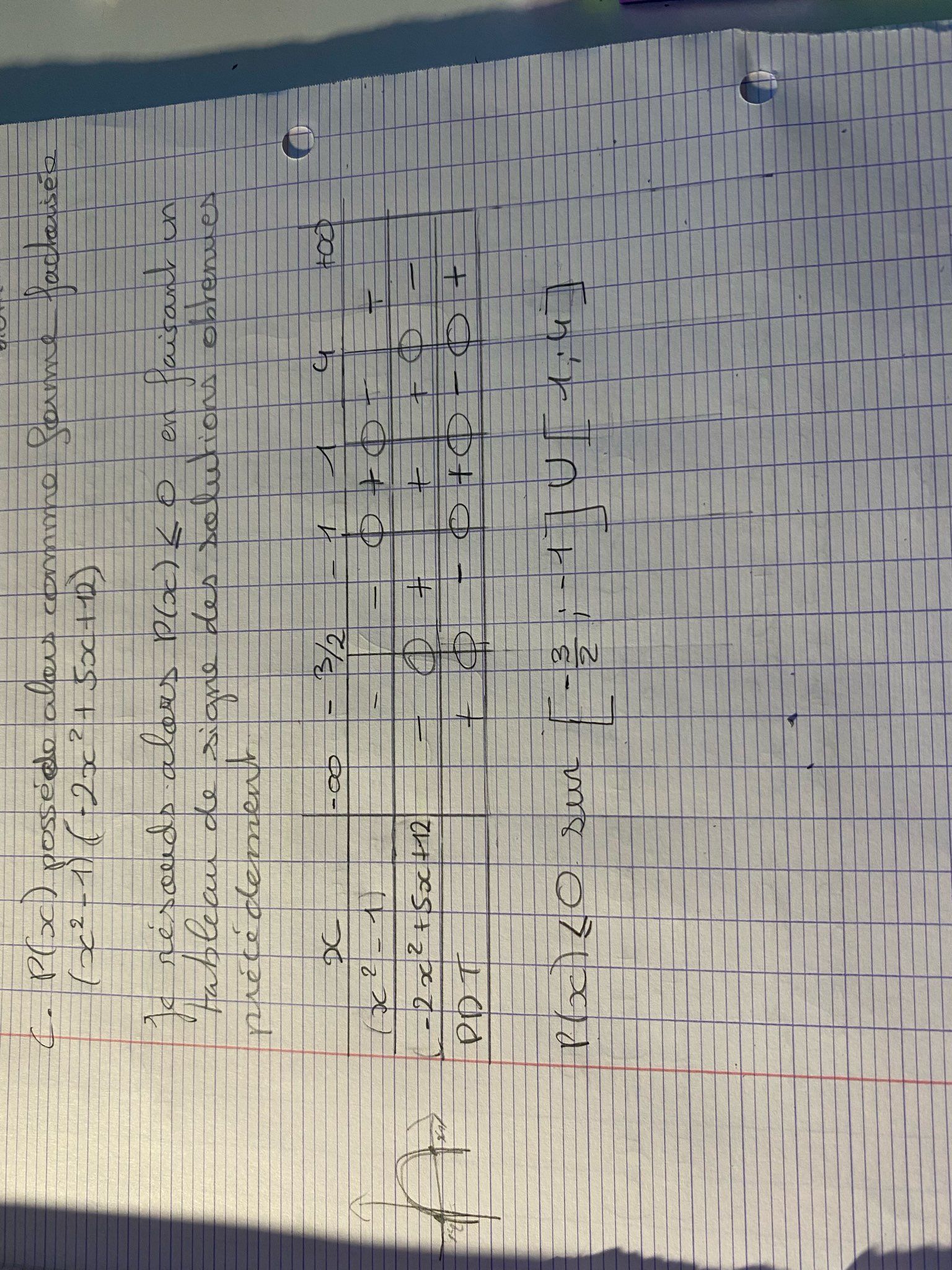
Tableau de signe.jpg
voilà

@Julie243554

Une erreur pour les signes de $x^2-1$ .

Je crois que c'est l'inverse, il faut que je mette + + - + +

Et donc P(x)<0 sur ]-infini ; -3/2]U[-1;1]U[4;+infini[ ?

@Julie243554

Oui pour les signes.
Pour la solution c'est pour $P(x)≤0P(x)\leq 0$ et non $P(x)<0P(x)\lt0$ .

Oui, je n'arrivais pas à mettre le signe égal

@Julie243554

Ok

Bonjour,

Pour info.

a)

Autre méthode (trop peu ou plus du tout enseignée ???)

P(x)= -2x^4 + 5x^3+14x^2-5x-12

On sait (par l'énoncé) que P(x) peut être factorisé par (x²-1) ... on s'arrange pour faire apparaître ce facteur.

Je le fais en plus que détaillé, mais avec un rien de pratique, c'est fait en 1 ligne ...

= -2x^4 + 2x² + 5x^3 + 12x^2-5x-12
= -2x^4 + 2x² + 5x^3 - 5x + 12x^2 -12
= -x²(2x²-2) + 5/2 x*(2x²-2) + 6(2x^2 -2)
= (2x²-2).(-x² + 2,5x + 6)

b)

P(x) = -2(x²-1)(x²-2,5x-6)
P(x) = -2(x-1)(x+1).[(x-1,25)²-1,25²-6]
P(x) = -2(x-1)(x+1).[(x-1,25)²-7,5625]
P(x) = -2(x-1)(x+1).[(x-1,25)²-2,75²]
P(x) = -2(x-1)(x+1).(x-1,25-2,75).(x-1,25+2,75)
P(x) = -2(x-1)(x+1).(x-4).(x+1,5)

c)
A partir de : P(x) = -2(x-1)(x+1).(x-4).(x+1,5), le tableau de signes est alors immédiat ...