Suites numériques (Maths complémentaires)

Bonsoir,
Je suis en mathématiques complémentaires et j'aurai besoin d'aide s'il vous plait

Exercice 1

Une somme de 1000 euros est placée à intérêts composés au taux de 0,2% par mois.
Soit (un le capital disponible au bout de N mois.

Exprimer u(n+1) en fonction de u(n) pour tout entier naturel u(n)
En déduire la nature de u(n)
Donner alors une formule explicite donnant u(n) en fonction de n pour tout entier n
Déterminer lim u(n) (avec n qui tend vers +oo)
Donner le sens de variation de u(n).
Soit A un nombre donné quelconque. Il existe une valeur de n à partir de laquelle tous les termes u(n) sont supérieurs à A . Pourquoi?
Ecrire l'algorithme d'une fonction de paramètre A donné, appelée min(A) qui renvoie le plus petit rang n(0) à partir duquel u(n) est supérieur à A
Ecrire en PYTHON un programme convenable pour la fonction min(A) . Que renvoie cette fonction pour A=1100?

Voici mes réponses:

u(n)= 1000 fois 1,02^n
u(n+1)= 1000 fois 1,02^n+1
La suite u(n) est une suite géométrique de raison 1,02 et de premier terme u(0)= 1000
Pour la formule explicite : u(n)= u(0) fois q ^n
ou u(n) = u(p) fois q^n-p
lim 1000= 1000
n tend vers +oo
lim 1,02^n = +oo car 1,02 plus grand que 1
n tend vers +oo
Par produit lim u(n) = +oo
n tend vers +oo
La suite u(n) est une suite qui converge
Car u(0) est toujours égal à 1000

Pour la question 4 je ne suis pas sûre et le reste des questions je n'y arrive pas
Merci d'avance

@maybessa Bonsoir,

Pour la question 3, c'est le sens de variation qui est demandé, donc suite croissante
Pour la question 4, prendre en compte les résultats obtenus aux question 2 et 3.

@maybessa , bonjour,

Je t'avance un peu plus ton exercice.

Bien sûr, dans la réponse à la 3) que tu as proposée, il y a une contradiction.
Puisque tu as prouvé que $U_n$ tend vers $+∞+\infty$ , cette suite ne peut pas être convergente. Ell est divergente.

Vu que le premier terme est strictement positif et que la raison est strictement supérieure à 1, elle est croissante.

Piste pour la 4)

Comme la suite tend vers $+∞+\infty$ , à partir d'un certain rang, elle prendra forcément des valeurs supérieures à A.

Ce n'est pas écrit dans l'énoncé, mais la question a un sens lorsque ce nombre A donné est plus grand que 1000.

Tu dois résoudre $Un>AU_n\gt A$ .

$1000×(1.02)n>A1000\times (1.02)^n \gt A$

$(1.02)n>A1000(1.02)^n \gt \dfrac{ A}{1000}$

J'espère que tu connais les logarithmes.

$nln(1.02)>ln(A1000)nln(1.02)\gt ln(\dfrac{ A}{1000})$

Vu que $l n (1.02)$ est srictement positif car $\gt 1$

on peut déduire :

$n>ln(A1000)ln(1.02)\boxed{n\gt \dfrac{ ln(\dfrac{ A}{1000})}{ln(1.02)}}$

Si tu préfères, tu peux écrire :

$n>ln(A)−ln(1000)ln(1.02)\boxed{n\gt \dfrac{ ln(A)-ln(1000)}{ln(1.02)}}$

Le plus petit rang $n_0$ à partir duquel $U_n$ est supérieur à A doit être un naturel.
C'est donc le plus petit naturel supérieur à $ln(A)−ln(1000)ln(1.02)\dfrac{ ln(A)-ln(1000)}{ln(1.02)}$

Un exemple pour comprendre :
Soit $A = 2000$ . avec la formule donnée, la calculette donne $n>35,0028n\gt 35,0028$
On prend donc $n_0=36$

En écriture mathématique, si tu connais la définition de partie entière notée $E$ ,
$n0=E(ln(A)−ln(1000)ln(1.02))+1n_0=E\biggr(\dfrac{ ln(A)-ln(1000)}{ln(1.02)}\biggr)+1$

@mtschoon
Bonsoir merci pour vos aides,
Malheureusement, je n'ai pas faire les logarithmes donc je ne saisis pas vraiment.
On sait que la suite à une limite qui tend vers plus l'infini et qu'elle est croissante donc elle sera toujours plus grande que A?

Ils sont supérieurs grâce à la raison?

@maybessa

Ils sont supérieurs car la suite tend vers $+∞+\infty$ .

@maybessa ,
Je pensais que , étant en Terminale, les logarithmes auraient été vu...
Dommage...

Evidemment, A étant un nombre (supérieur à 1000) et la suite étant croissante et tendant vers $+∞+\infty$ , à partir d'un certain rang $n_0$ , les termes de la suite seront forcément supérieurs à A.

@mtschoon

Merci donc comment l'algorithme doit il être composé ?

@maybessa , je regarderai demain si besoin.

L'idée sera de faire calculer les termes $U_n$ jusqu'au premier terme qui dépasse A et faire afficher la valeur $n_0$ de ce terme.

Mais ce n'est que l'idée.
Il faudra faire un algoritme soigné.

@maybessa , bonjour,

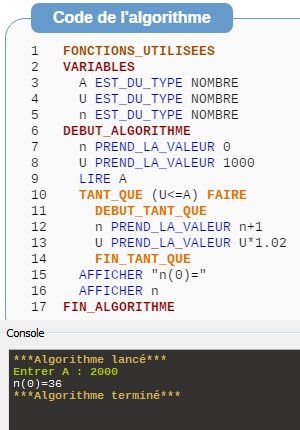
Je te joins un algorithme tapé avec Algobox ( logiciel gratuit que tu peux télécharger), utilisant la boucle TANT QUE.
Il a l'avantage de tester pour pouvoir vérifier qu'il n'y a pas d'erreur.

Dans cet algorithme,

L'utilisateur donne la valeur de A de son choix (mais il faut qu'il le choisisse une valeur supérieure à 1000 )

Pour $n = 0$ , $U = 1000$
Tant que $U≤AU\le A$ , $U$ est calculé avec la formule $Un+1=Un×1.02U_{n+1}=U_n\times 1.02$ qui s'écrit ici : $U$ prend la valeur $U×1.02U\times 1.02$

Je l'ai fait tester avec la valeur A=2000 (comme dans l'explication donnée précédemment)

Bien sûr, il faudra l'écrire à la façon de ton professeur.!

@mtschoon Bonjour,

Merci concernant l'application,
Par rapport à l'algorithme vous avez marqué que tant que u est inférieure à A alors que dans la question il est dit que u doit être supérieur à A?
Donc je ne comprends pas
Merci d'avance

@maybessa ,

Le programme "tourne" tant que U est inférieur ou égal à A et il affiche la plus petite valeur de n appelée n(0) telle que U > A

Pour comprendre, tu peux faire les calculs "à la main" en choisissant une valeur de A pas trop grande.

Par exemple, si tu prends A=1070
Tu dois trouver :
$U_1=1020$
$U_2=1040.4$
$U_3=1061.2$
$U_4=1082.4$

la boucle "Tant que" calcule successivement $U_1, U_2,U_3$ et à $n = 4$ , l'ago voit que la valeur $U_4$ est supérieure à 1070 donc il s'arrète, et l'algo affiche la valeur 4 (qui est la première valeur de n pour laquelle la suite a une valeur supérieure à 1070) .

@mtschoon bonsoir ,
Je comprends mieux mercii

@maybessa , c'est très bien de mieux comprendre ;
Evidemment, ce serait parfait si tu comprenais en totalité.

J'essaie de te détailler ce que fait le programme du "Début de l'algorithme" juqu'a la "Fin de l'algorithme"

n=0
U=1000
Lire A veut dire que l'utilisateur donne A qui sera lu par le programme.
Je choisis A=1070

On rentre dans la boucle " Tant que"
Vu que n valait 0, n prend la valeur n+1 veut dire que n=0+1=1
Vu que U valait 1000, U prend la valeur $U×1.02U\times 1.02$ veut dire que $U=1000×1.02=U=1000\times 1.02=$ 1020
Vu que $\le 1070$ , on fait un autre "tour de boucle" c'est à dire qu'on remonte au début de la boucle.

Vu que n valait 1, n prend la valeur n+1 veut dire que n=1+1=2
Vu que U valait 1020, U prend la valeur $U×1.02U\times 1.02$ veut dire que $U=1020×1.02=U=1020\times 1.02=$ 1040,4
Vu que $\le 1070$ , on fait un autre "tour de boucle" , c'est à dire qu'on remonte au début de la boucle.

Vu que n valait 2, n prend la valeur n+1 veut dire que n=2+1=3
Vu que U valait 1040,4, U prend la valeur $U×1.02U\times 1.02$ veut dire que $U=1040,4×1.02=U=1040,4\times 1.02=$ 1061,2
Vu que $\le 1070$ , on fait un autre "tour de boucle" c'est à dire qu'on remonte au début de la boucle.

Vu que n valait 3, n prend la valeur n+1 veut dire que n=3+1=4
Vu que U valait 1061,2, U prend la valeur $U×1.02U\times 1.02$ veut dire que $U=1061,2×1.02=U=1061,2\times 1.02=$ 1082,4
Vu que $\gt 1070$ , la boucle "Tant que" s'arrête et on sort de la boucle" Tant que".

Le programme exécute ensuite ce qu'il y a écrit après "Fin de Tant que" , c'est à dire Afficher n : la dernière valeur de n est 4 donc le programme affiche la valeur 4

(J'ai fait écrire n(0)=4 pour que ça soit plus lisible)

J'ai fait le mieux possible.

Bonne lecture.

@mtschoon a dit dans Suites numériques (Maths complémentaires) :

Bien sûr, il faudra l'écrire à la façon de ton professeur.!

bonsoir
c'est quel logiciel?

Bonjour,

Cela a été indiqué :

@mtschoon a dit dans Suites numériques (Maths complémentaires) :

Je te joins un algorithme tapé avec Algobox ( logiciel gratuit que tu peux télécharger),

@mtschoon

Mercii pour le détail de l'explication,
J'essayer de le faire avec le programme python
Mais je le trouve assez compliqué ça a la moindre erreur il ne marche pas

Def u(n)
U= 1000
For i in range (1, n+1)
U= 1000* 1,02^n

   Return u

C'est ça je ne sais pas comment inclure le tant que?

@maybessa , bonjour,

J'ai dû te le dire sur un autre topic , je ne suis pas spécialiste du Python, mais Tant que se traduit par while.