Bonjour à tous j'aimerais savoir comment déterminer les points d'intersection d'une courbe a l'axe des abscisse avec cette fonction f(x)=(2x³+2x²-10x+11)/(2(x-1)²) merci bien pour votre aide

Re : Fonction : Intersection avec les axes. Etude. Tangentes.~~texte en gras~~

@Kobenan-Desnoce-Yao , bonjour,

Si j'ai bien lu :

$f(x)=2x3+2x2−10x+112(x−1)2f(x)=\dfrac{2x^3+2x^2-10x+11}{2(x-1)^2}$

D'abord, tu travailles sur $D = R$ \ {1} ( pour que le dénominateur ne soit pas nul ).

Tu dois résoudre $f (x) = 0$

Cela revient à résoudre : $2x^3+2x^2-10x+11=0$

Equation du 3ème degré sans solution évidente.

Il y a bien sûr des formules ( avec de racines cubiques ) mais cela est tout à fait hors programme.

Tu dois chercher une autre voie.

Tu peux étudier la fonction sur $D$

Tu trouveras ainsi que pour $\gt 1$ , $\gt 0$ donc pas de solution à $f (x) = 0$ .

Pour $x<1x\lt 1$ , f est continue et strictement croissante et varie de $−∞-\infty$ et + $∞\infty$ .
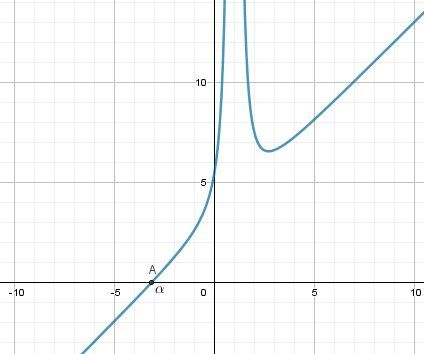
Donc un point d'intersection avec l'axe des abscisses ( pour légitimer cela , il y a le théorème des valeurs intermédiaires, mais en principe, on l'étudie en Terminale).

Pour trouver une valeur approchée de l'absisse $α\alpha$ de ce point, tu utilises ta calculette.
$α≈−3.14548\alpha \approx -3.14548$

Illustration graphique