Exercice sur les fonction polynomiales

Bonjour,
f et g deux conctions définies sur R,
f(x)=ax^2 +bx +c, x apparient a R étoile et b,c appartiennent a R, on suppose f>0 quelque soit x dans R,
laquelle des supposition suivantes est vrai, g>0, g<0, g=0, il existe x dans R tel que g(x)=0

@Mohssine Bonjour,

Quelle est l'expression de la fonction $g$ ?

Bonjour, pardon g=f+f'+f''

@Mohssine

Indique tes calculs.
Donne l'expression de $g (x)$ en fonction de $a$ , $b$ et $c$ .

Bonjour,

@Mohssine , un petit plus, si besoin, pour avancer.

$g(x)=f(x)+f'(x)+f''(x)=ax^2+bx+c+2ax+b+2a$
En regroupant les termes, tu dois obtenir
$g(x)=ax^2+(b+2a)x+(2a+b+c)$

Par hypothèse, $f(x)>0f(x)\gt 0$ pour tout x réel

Cela se traduit par $Δ<0\Delta \lt 0$ ( pour que l'équation $f (x) = 0$ n'ait pas de solution) et $a>0a\gt 0$ pour que $f (x)$ soit toujours strictement positif (signe de a)
Tu as donc deux conditions : $b2−4ac<0\boxed{b^2-4ac \lt 0}$ et $a>0\boxed{a\gt 0}$
Tu pourras te servir de ces deux conditions pour analyser g

Pour analyser g, tu peux calculer son discriminant et déterminer le signe de son discriminant.
Cela te permettra de tirer une conclusion.

Bonjour,
g positive?

@Mohssine ,

Je pense que Oui, mais il faut que tu fasses le calcul du discriminant de g .

Si tu as prouvé que ce discriminant ( de g) est strictement négatif, g sera toujours du signe de a (coefficient de $x^2$ ) donc positif pour tout x réel.

@mtschoon elle semble positive mais la preuve reste a montrer; ce qui est but le l exercice je crois

@Mohssine , oui tout à fait , c'est le but de l'exercice.

C'est ce que je viens de t'expliquer :

Tu calcules le discriminant de g
Tu prouves qu'il est strictement négatif et tu tires la conclusion.

Remarque : pour que tu puisses vérifier ton calcul, je t'indique le discriminant de g que je viens de calculer

Après simplifications :

$Δg=b2−4ac−4a2\Delta_g=b^2-4ac-4a^2$

$Δg=(b2−4ac)−4a2\Delta_g=(b^2-4ac)-4a^2$

$b^2-4ac$ est le discriminant de f que tu sais strictement négatif , donc tu peux tirer facilement la conclusion utile.

@mtschoon Merci j fais les calculs, mais le descriminant negative veut dire l equation g=0 n'dmet pas de solution, comment on deduit que g postive?

@Mohssine ,

Regarde ici pour le signe d'un polynôme due second degré
C'est le paragraphe II
https://www.mathforu.com/premiere-s/le-second-degre-2eme-partie/

Lorsque que le discriminant est strictement négatif, le polynôme est du signe du coefficient de x² (c'est à dire a)

Comme ici a est positif ( c'est aussi le coefficient de x² du polynôme f ), tu peux déduire que pour tout x réel , $g(x)>0g(x)\gt 0$

Revois tout ça de près.

@mtschoon j ai vue ca mais il y a pas de demonstration

@Mohssine , il n'y a pas de démonstrations car ce sont des propriétés usuelles démontrées en cours donc ce sont des théorèmes que l'on utilise directement.

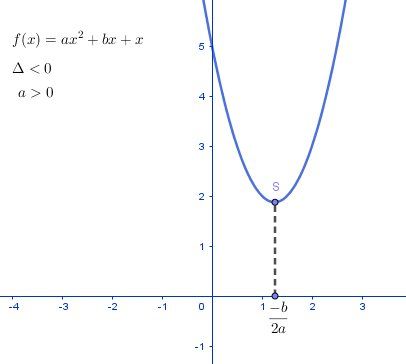
@Mohssine , si tu veux une explication "imagée", pense que la représentation graphique d'une fonction polynôme du second degré (f(x)=ax²+bx+x) est une parabole (P)

Lorsque $Δ\Delta$ est strictement négatif , pas de solution à l'équation f(x)=0.
La parabole ne coupe pas l'axe des abccisses ; elle est au-dessus ou au dessous.

Si $a>0\boxed{a\gt 0}$ , la parabole a sa concacité tournée vers le haut, elle est au-dessus de l'axe des abscisses : $\gt 0$

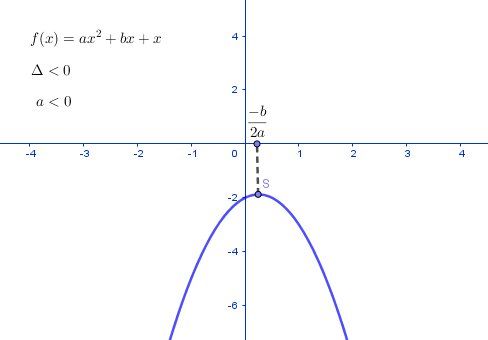
Si $a<0\boxed{a\lt 0}$ , la parabole a sa concacité tournée vers le bas, elle est au-dessous de l'axe des abscisses : $\lt 0$

@mtschoon merci c est compris, ca se démontre géométriquement comme vous avez mentioné, j ai autres exercices que j posté et j attends que vous m aider sur eux et je te remercie d avance

@Mohssine , ça se démontre géométriquement mais ça se démontre aussi analytiquement en passant par la forme canonique, mais pour comprendre, il me semble que géométriquement c'est plus clair.

Bonjour,

Alternative sans calculer le discriminant de g.

f(x)=ax^2 +bx +c
f > 0 pour tout x impose : a > 0 et b²-4ac < 0

f(x)=ax^2 +bx +c
f'(x) = 2ax + b
f''(x) = 2a

f(x) + f'(x) + f''(x) = a.x^2 + (2a+b).x + 2a + b + c

g(x) = a.x^2 + (2a+b).x + 2a + b + c (Avec a > 0 et b²-4ac < 0)

Extremum de g(x) pour x = -(2a+b)/(2a)

Cet extremum vaut g(-(2a+b)/(2a)) = a*(-(2a+b)/(2a))² + (2a+b)*(-(2a+b)/(2a)) + 2a + b + c

= (4a²+b²+4ab)/(4a) - (4a²+b²+4ab)/(2a) + 2a + b + c

= -(4a²+b²+4ab)/(4a) + 2a + b + c

= (-4a²-b² - 4ab + 8a² + 4ab + 4ac)/(4a)

= (4a² - b² + 4ac)/(4a), or a > 0 et b²-4ac < 0 ---> = (4a² - b² + 4ac)/(4a) > 0

L'extremum est positif

On a donc une parabole avec la concavité tournée vers le haut (car a > 0) et dont l'extremum (qui est un minimum) est > 0

Donc g(x) = 0 n'a pas de solution, g est partout > 0

Illustration graphique