Recherche de l'existence de tangente passant par un point donné

Bonsoir
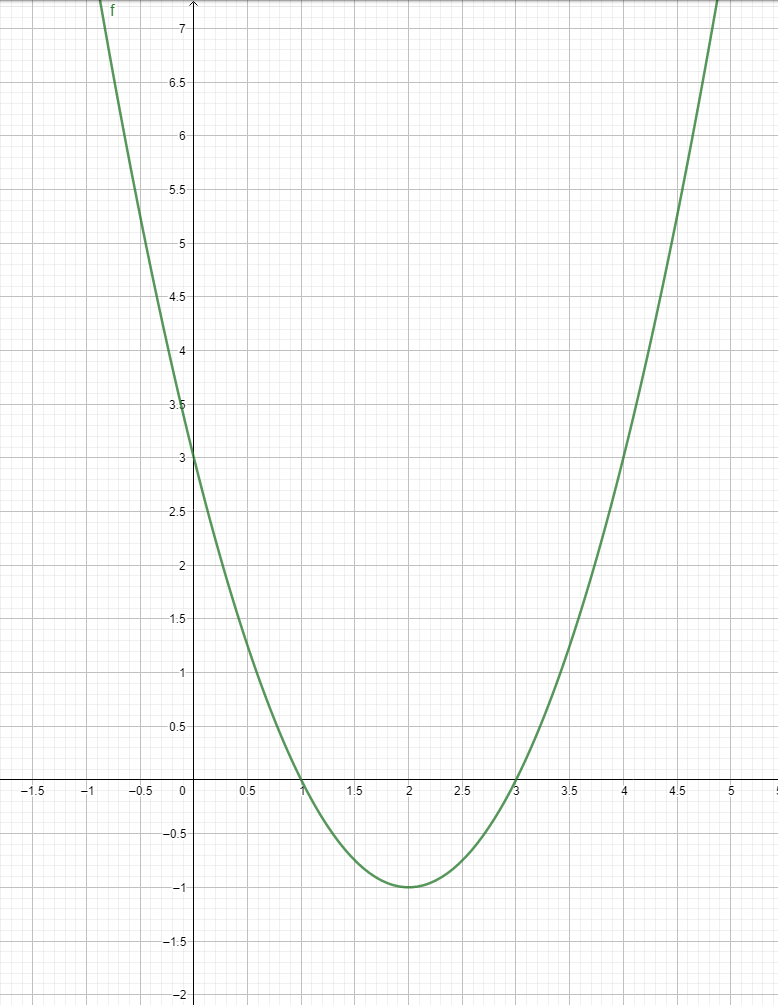
On considère la fonction f définie par f(x) = x²- 4x + 3.

On appelle C sa courbe représentative dans le repère ci-dessous ( en pièce joint )

a) Monter que l'équation de la tangente T à C en un de ses point M d'abscisse a est y = ( 2a - 4) x - a² + 3
( je l'ai fait mais je l'ecrit quand même au cas ou )

b) Montrer qu'il existe deux tangentes a C passant par le point A( 5/2 ; - 3 )

Merci d'avance à celles et à ceux qui se pencheront sur mon problème ...

[texte du lien] 2021-11-06 (3).png

Bonjour,

Equation de la tangente à la courbe au point d'abscisse a :

Ta : y = (2a-4)x - a² + 3 (1)

Si la tangente passe par le point A(5/2 ; -3), on a :

-3 = (2a-4)*5/2 - a² + 3

-3 = (5a-10) - a² + 3

a² - 5a + 4 = 0

... qui va donner 2 valeurs possibles de a

et en remettant ces valeurs dans (1) ... tu auras les équations des 2 tangentes à C passant par le point A

@Denzen-Yumi Bonjour (Marque de politesse à ne pas oublier !!)

Indique un titre significatif au sujet.

Pour la question b),
tu utilises la réponse à la question a).
Tu utilises les coordonnées du point A et tu résous l'équation d'inconnue $a$ .
Tu dois trouver deux valeurs pour $a$ .

Ce message a été supprimé !

@Noemi ouiii pardon dans la précipitation je l'ai oublier je vous remerci de votre aide passez une bonne soirée

@Black-Jack exusez-moi mais je n'ai pas très bien compris ce qu'il faut faire et pourquoi c'est x que l'on remplace dans le (1)
car si l'on cherche le coefficiant directeur de la tangeante, ne faut-t-il pas garder le x ?

@Denzen-Yumi

Le point A appartient à la tangente, donc ses coordonnées vérifient son équation.

Ce message a été supprimé !

Bonjour,

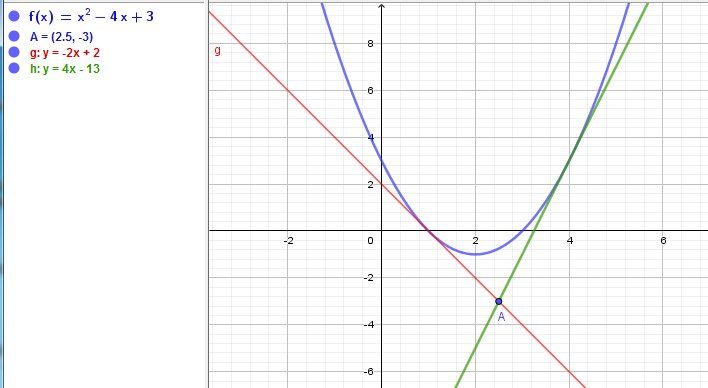
Illustration graphique.

Equation d'une tangente quelconque : $y=(2a-4)x-a^2+3$
Une tangente passe par $A (5 / 2, - 3)$ : $a$ solution de $a^2-5a+4=0$ c'est à dire $a =$ 1 ou $a = 4$
D'où :
Pour $a = 1$ , tangente (rouge) d'équation $y = - 2 x + 2$ passant par $A (5 / 2, - 3$ )
Pour $a = 4$ , tangente (verte) d'équation $y = 4 x - 13$ passant par $A (5 / 2, - 3)$