Exercice sur les suites pour un DM

Bonjour !
J'ai un exercice, dans mon DM de maths niveau première, qui porte sur les suites, et dont j'ai du mal à faire les questions 5 et 6, même si je pense les avoir comprises.

Pourriez-vous m'éclairer sur ce qui est demandé, et éventuellement suggérer des solutions / expliquer svp ?

Scan supprimé par la modération. Pour obtenir des pistes de résolution, l'énoncé doit être écrit.
Une aide pour l'écriture des relations en Latex :
$un=2nn2u_n=\dfrac{2^n}{n^2}$
$n2−2n−1≥0n^2-2n-1\geq0$

@arimotoka476 , bonjour,

Ici, les scans d'énoncés ne sont pas autorisés, sauf pout graphiques ou tableaux.
Pour avoir de l'aide, il faut écrire ton énoncé.

Je l'aurais bien fait, mais je n'ai aucune idée de comment écrire les formules pour qu'elles soient compréhensibles.

@arimotoka476 , je te mets un lien pour écrire les formules en Latex, mais tu peux faire le mieux possible sans Latex, on arrive à comprendre.

https://forum.mathforu.com/topic/163/comment-écrire-les-principales-expressions-mathématiques-work-in-progress

@arimotoka476 ,
En fonction des deux indications écrites, je t 'indique , si cela t'est utile, les premiers termes de la suite (valeurs approchées)

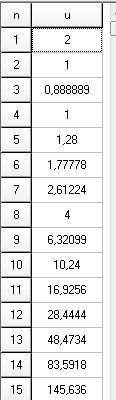
On peut constater que cette suite n'est pas monotone.
On peut conjecturer qu'elle est croissante à partir de n=3

Sur $R$ , l'inéquation $n2−2n−1≥0n^2-2n-1\ge 0$ a pour solutions :
$n∈]−∞,1−2]∪[1+2,+∞[n\in ]-\infty, 1-\sqrt 2] \cup[1+\sqrt 2,+\infty[$

$1−2≈−0.4141-\sqrt 2 \approx -0.414$
$1+2≈2.4141+\sqrt 2 \approx 2.414$

Sur $N^*$ , les solutions sont donc les naturels supérieurs ou égaux à $3$

Si tu veux d'autres renseignements, écris ton énoncé.

@mtschoon
Très bien. Merci pour le lien et pour ce début de résolution, j'en étais à vrai dire arrivée jusque là.
Ce qui me pose problème, c'est la suite :
Il m'est demandé de déterminer un entier $n$ naturel tel que $un0≥1050u_{n0} \geq 10^50$ (c'est exposant 50, j'ai du mal à l'afficher).
...et de justifier ensuite que pour tout $\geq n_{0}$ , on a $un≥1050u_{n} \geq 10^50$ (50.)

Pourriez-vous m'aider avec cela ?

@arimotoka476 Bonjour,

Pour déterminer $u_{n_0}$ , tu peux utiliser le tableur.
Sauf erreur : $n_0=182$ ,
Pour la justification il faut étudier les variations de la suite.

@arimotoka476 ,

Merci d'avoir écrit la suite de ton énoncé.

J'ai trouvé aussi que $n_{0}=182$

Vu que $10^{50}$ dépasse le seuil de capacité des calculettes ordinaires, il faut un outil plus perfectionné.

Il y a bien une autre méthode pour faire "baisser" l'exposant, c'est d'utiliser les logarithmes, mais tu postes en Première et les logarithmes s'étudient, dans les programmes français, en Terminale...

Je te l'indique pour le cas où tu connaîtrais les logarithmes...

Tu as le choix entre logarithme népérien ( noté ln )et logarithme décimal (noté log)
Vu qu'il s'agit de $10^{50}$ , le logarithme décimal est mieux adapté.

$Un0≥1050U_{n_0}\ge 10^{50}$ <=> $2n0(n0)2≥1050\dfrac{2^{n_0}}{(n_0)^2}\ge 10^{50}$ <=> $2n0≥(n0)2×1050\boxed{2^{n_0}\ge (n_0)^2\times 10^{50}}$

En prenant le logarithme décimal de chaque membre et en utilisant les propriétés usuelles de log, tu obtiens :
$n0log(2)≥2log(n0)+50n_0log(2) \ge 2log(n_0)+50$ <=> $n0log(2)−2log(n0)≥50\boxed{{n_0log(2) - 2log(n_0)\ge 50}}$

Avec la fonction"table" de ta calculette, ou une fonction de ta calculette prévue pour les les suites, tu dois trouver :

Pour $n = 181$ , $2log(n)\approx 49.971$
Pour $n = 182$ , $2log(n)\approx 50,267$

Tu peux donc prendre $n0=182\boxed{n_0=182}$

182 est la plus petite valeur de n telle que $Un≥1050U_n\ge 10^{50}$

Tu as dû démontrer dans une question précédente que la suite $U_n)$ est croissante à partir du rang 3

Donc :
Pour $n≥182\boxed{n\ge 182}$ , $Un≥U182≥1050U_n\ge U_{182} \ge 10^{50}$ , donc, par transitivité de la relation $≥\ge$ , tu peux conclure que $Un≥1050\boxed{U_n\ge 10^{50}}$

@Noemi
Merci pour l'idée ! Je vois ce que vous voulez dire

@mtschoon
Je ne connais effectivement pas les logarithmes.. Maintenant que vous en parlez je vais m'y intéresser mais je doute que mon professeur valide cette réponse.
Quoi qu'il en soit, merci beaucoup pour le temps accordé et pour cette explication plus que complète !

@arimotoka476 ,,

Effectivement, en Première (programme français) , on n'apprend pas les logarithmes. Tu attendras l'année prochaine.
Justifie ce $n_0=182$ avec tableur ou autre outil puissant. Tu n'as pas le choix...

Bon travail.