DM limites - fonctions de comparaison
-
suhn1 dernière édition par
f est la fonction définie sur R par f(x) = x*e^-x. On note Cf sa courbe représentative dans le plan muni d'un repère orthogonal. Justifier tout le tableau de variations de f :
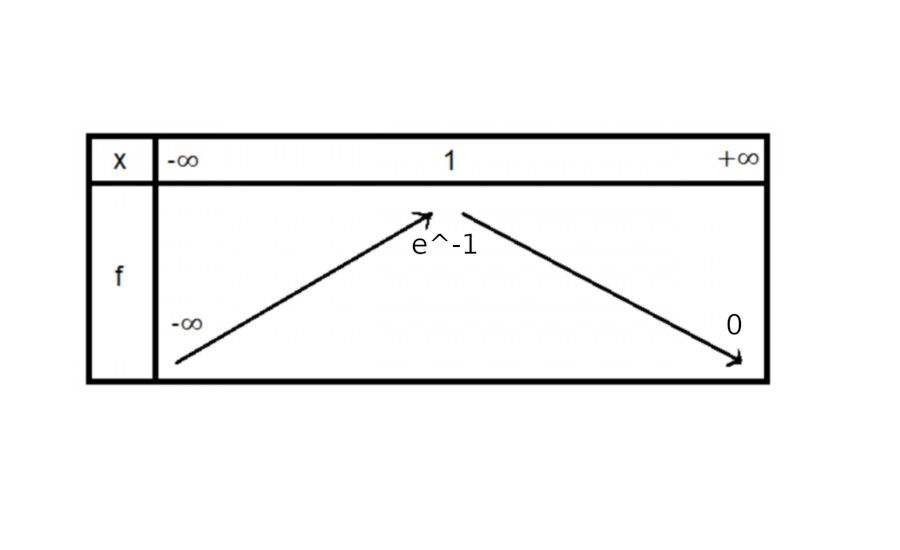(J'ai besoin d'aide je ne sais pas quoi utiliser pour faire cet exercice)
-
@suhn1 Bonsoir (Marque de politesse à ne pas oublier !!)
La dérivée de la fonction : f′(x)=e−x−xe−xf'(x) = e^{-x}-xe^{-x}f′(x)=e−x−xe−x
Factorise cette expression et étudie son signe, pour en déduire les variations.
-
mtschoon dernière édition par mtschoon
Bonjour,
@suhn1, je détaille un peu si tu n'es pas arrivé à solutionner ton problème.
f(x)=xe−xf(x)=xe^{-x}f(x)=xe−x
Pour la dérivée, tu as pris, je pense, la dérivée d'un produit
U(x)=xU(x)=xU(x)=x d'où U′(x)=1U'(x)=1U′(x)=1
V(x)=e−xV(x)=e^{-x}V(x)=e−x d'où V′(x)=(−1)e−x=−e−xV'(x)=(-1)e^{-x}=-e^{-x}V′(x)=(−1)e−x=−e−xTu sais que (UV)′=U′V+UV′(UV)'=U'V+UV'(UV)′=U′V+UV′
Après caclul, tu trouves f′x)=e−x−xe−x=e−x(1−x)f'x)=e^{-x}-xe^{-x}=e^{-x}(1-x)f′x)=e−x−xe−x=e−x(1−x)Pour tout x réel, e−x>0e^{-x}\gt 0e−x>0
Le signe de f'(x) est donc le signe de (1−x)(1-x)(1−x)f′(x)=0f'(x)=0f′(x)=0 <=> 1−x=01-x=01−x=0 <=> −x=−1-x=-1−x=−1 <=>x=1\boxed{x=1}x=1
Tu calcules f(1)f(1)f(1) et tu trouves e−1e^{-1}e−1f′(x)<0f'(x)\lt 0f′(x)<0 <=> 1−x<01-x\lt 01−x<0 <=> −x<−1-x\lt -1−x<−1 <=>x>1\boxed{x\gt 1}x>1
donc f décroissante.f′(x)>0f'(x)\gt 0f′(x)>0 <=> 1−x>01-x\gt 01−x>0 <=> −x>−1-x\gt -1−x>−1 <=>x<1\boxed{x\lt 1}x<1
donc f croissante.Pour les limites,
Lorque x tend vers −∞-\infty−∞, −x-x−x tend vers +∞+\infty+∞, donc e−xe^{-x}e−x tend vers +∞\infty∞
Vu que x tend vers −∞-\infty−∞, le produit tend vers −∞-\infty−∞
limx→−∞f(x)=−∞\boxed{\displaystyle \lim_{x\to -\infty}f(x)=-\infty}x→−∞limf(x)=−∞Lorque x tend vers +∞+\infty+∞, pour te ramener à une limite usuelle, tu peux transformer f(x)f(x)f(x).
f(x)=xex=1(exx)f(x)=\dfrac{x}{e^x}=\dfrac{1}{\biggr(\dfrac{e^x}{x}\biggr)}f(x)=exx=(xex)1
Par théorème : limx→+∞exx=+∞\displaystyle \lim_{x\to +\infty}\dfrac{e^x}{x}=+\inftyx→+∞limxex=+∞ donc ,limx→+∞f(x)=0\boxed{\displaystyle \lim_{x\to +\infty}f(x)=0}x→+∞limf(x)=0
Bonnes réflexions.
