Exercice Asymptote oblique

Bonjour pouvez-vous m’aider pour cet exercice s’il vous plaît
On considère la fonction F(x) = (x^2 + x - 6) / (2x - 2)
Déterminer l’existence de trois réels a, b, et c tels que
F(x) = ax + b + c/2x-2
En déduire l’existence d’une asymptote oblique dont on précisera une équation.

@RK Bonjour,

Réduis l'expression $ax+b+c2x−2ax+b+\dfrac{c}{2x-2}$ au même dénominateur puis identifie terme à terme avec l'expression initiale.

Regarde ce cours : https://www.mathforu.com/premiere-s/l-identification-pour-une-fonction-rationnelle/

@RK
Pouvez-vous me dire si mes réponses sont justes svp
1er partie : j’ai la rédaction sur ma copie
Mais voilà mes résultats : a=1; b=3/2; c=2
Donc f(x) = x + 3/2 + 2/(2x-2)
2ème Partie :
F(x) - (ax+b) = c/2x-2
<=> f(x) - (x + 3/2) = 2/(2x-2)
Lim 2/(2x-2) =0 quand x tend vers +l’infini
Donc lim f(x) quand x tend vers +l’infini =0
Donc f(x) est une asymptote oblique d’équation y= 2/(2x-2)
Voilà juste je suis pas sûr pour l’équation
Mercii

@RK

C'est faux, vérifie tes calculs
Tu dois trouver le système :
${2a=1−2a+2b=1−2b+c=−6\begin{cases} 2a=1 \cr-2a+2b=1 \cr -2b+c=-6 \end{cases}$

Bonjour,

Alternative (pas enseignée ???)

F(x) = (x^2 + x - 6) / (2x - 2)
F(x) = (1/2) * (x^2 + x - 6) /(x - 1)
F(x) = (1/2) * (x^2 - x + 2x -2 - 4) /(x - 1)
F(x) = (1/2) * (x(x-1) + 2(x -1) - 4) /(x - 1)
F(x) = (1/2) * (x + 2 - 4/(x - 1))
F(x) = (1/2).x + 1 - 4/(2x-2)

Pour l'asymptote oblique, réfléchis ... mieux que dans ton message précédent.

@Noemi
J’ai trouvé à=1/2
b=1
c=3

@RK

Une erreur pour c
${2a=1−2a+2b=1−2b+c=−6\begin{cases} 2a=1 \cr-2a+2b=1 \cr -2b+c=-6 \end{cases}$
${a=12−2a+2b=1−2b+c=−6\begin{cases} a=\dfrac{1}{2} \cr-2a+2b=1 \cr -2b+c=-6 \end{cases}$
${a=12b=1−2b+c=−6\begin{cases} a=\dfrac{1}{2} \cr b=1 \cr -2b+c=-6 \end{cases}$
${a=12b=1−2+c=−6\begin{cases} a=\dfrac{1}{2} \cr b=1 \cr -2+c=-6 \end{cases}$
${a=12b=1c=−6+2=−4\begin{cases} a=\dfrac{1}{2} \cr b=1 \cr c=-6+2=-4 \end{cases}$

L'asymptote oblique de la forme $y = a x + b$ est .....

Bonjour,

@RK , lorsque tu auras bien compris et refais les calculs, il serait bon que tu réalises ce qu'est l'asymptote oblique.

Illustration graphique,

$f(x)=12x+1−42x−2f(x)=\dfrac{1}{2}x+1-\dfrac{4}{2x-2}$ courbe en bleu
$x = 1$ droite en rouge , asymptote "verticale" correpondant à la valeur interdite x=1 ( car on ne peut pas diviser par 0)
$y=12x+1y=\dfrac{1}{2}x+1$ , droite (D) en vert , asymptote oblique
(Lorsque x tend vers + $∞\infty$ ou - $∞\infty$ , $42x−2\dfrac{4}{2x-2}$ tend vers 0, et la droite (D) est de plus en plus "proche" de la courbe en bleu).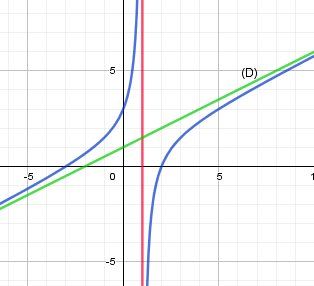

Bonnes réflexions.