Position d'une courbe par rapport à sa tangente

Bonjour

Dans mon exercice, une question me pose probleme

Dans un premier temps, j'ai calculé l'équation de la tangente au point d'abscisse 2 de
f(x)=2x^2-3x+2 et j'ai trouvé y=5x-6

Ensuite j'ai tracer la courbe C et la tangente sur ma calculatrice et la question qui me pose problème est : "Conjecturer la postion de C par rapport à T"

Est ce que je dois parler d'un intervalle et dire que C est croissante ou au dessus de T ?
Merci d'avance

@Livindiam-Livin , bonjour,

Tu étudies le signe de la différence $f (x) - (5 x - 6)$

Après calcul , sauf erreur, tu dois trouver :
$f(x)-(5x-6)=2x^2-8x+8=2(x^2-4x+4)=2(x-2)^2$

Tu tires la conclusion.

Reposte si besoin.

@mtschoon Sachant que dans cette question il m'est demandé de conjecturer, dois-je faire directement un tableau de signe ou dois je d'abord conjecturer que C sera au dessus de T ?

Les questions suivantes demandent par ailleurs de calculer f(x)-(5x-6) où j'ai trouvé le même résultat (2(x-2)^2) puis la dernière question est de démontrer la conjecture de la question 2 ( celle où il faut conjecturer)

En espérant avoir été clair

@Livindiam-Livin Bonjour,

Pour la conjecture, tu précises par exemple que d'après les représentations graphiques, le graphe de la fonction est au dessus de celui de la tangente.
Tu écris ensuite le calcul de $f (x) - (5 x - 6)$ ;
Tu conclus ensuite par analyse du résultat précédent sur la conjecture.

@Noemi c'est compris merci !

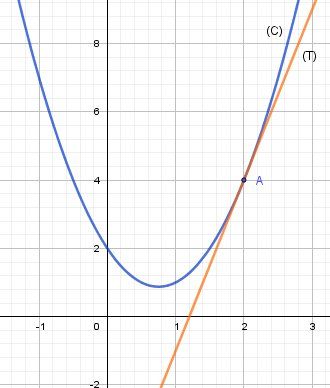
Graphique.

(C) : $f(x)=2x^2-3x+2$
(T) : $y = 5 x - 6$
$f(x)-(5x-6)=2(x-2)^2$

Pour $x = 2$ : (C) touche (T)
Pour $x≠2x\ne 2$ : (C) au dessus de (T)

=@mtschoon Est ce que la courbe est toujours au dessus de la tangente sauf lorsque x=2 ?

@Noemi Re bonjour, dois-je faire un tableau de signe ?

@Livindiam-Livin

Un tableau de signes n'est pas indispensable car $2(x−2)2≥02(x-2)^2\geq0$ .

@Livindiam-Livin a dit dans Position d'une courbe par rapport à sa tangente :

=@mtschoon Est ce que la courbe est toujours au dessus de la tangente sauf lorsque x=2 ?

Tout à fait @Livindiam-Livin

Vu que $f(x)-(5x-6)=2(x-2)^2$ ,
Pour $x≠2x\ne 2$ ,
$(x−2)2>0(x-2)^2 \gt 0$ donc $2(x−2)2>02(x-2)^2 \gt 0$ donc $f(x)−(5x−6)>0f(x)-(5x-6)\gt 0$ donc $f(x)>(5x−6)f(x)\gt (5x-6)$ donc (C) au dessus de (T)

Tu dois le "voir" sur le graphique.
Choisis un point A quelconque sur l'axe des abscisses (avec $xA≠2x_A\ne 2$ ), et trace la droite (d) parallèle à l'axe des ordonnées, passant par A.
(d) coupe (C) en M et (T) en P
Tu as toujours M au-dessus de P vu que $yM>yPy_M\gt y_P$
( $y_M=f(x)$ et $y_P=5x-6$ )