exercices : Distance point-droite

Bonjour,
J'aurais besoin d'aide pour un exercices en mathématique (dont j'ai déjà répondu a la première question)

Déterminer l’équation de la parabole ayant pour directrice d=>3x-4y=0 et pour foyer A :(-1,0).
Détermine la coordonnée de son sommet.
Détermine l’équation de son axe de symétrie

=> Réponses finale :
p=16x²+9y²-24xy=0
-> Pour le sommet on a une fonction avec 2 carré c'est ce qui me pose problème

@Joyca-Le-Boss

Pour le sommet
α =-b/2a => -9/32 α(-9/32)
et β = -Δ/4a
Δ<0 => 0 sol

@Joyca-Le-Boss Bonjour,

Vérifie le calcul pour l'équation de la parabole, tu ne dois pas avoir de $y^2$ ou de $x^2$ .

@Noemi bonjour, j'ai toujours le y² dans mon équation

@Joyca-Le-Boss

Indique tes calculs.

@Noemi voici mes calculs :

Bonjour,

Je n'ai pas vérifié tes calculs ... mais l'équation que tu donnes est bien celle d'une parabole. (mais son axe est oblique, ce qui est normal puisque la directrice est aussi oblque.

Théorie :

La forme générale des équations des coniques est : Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0

Si on a AC-B² = 0 ... c'est une parabole (et c'est le cas ici) avec A = 16, B = -12, et C = 9

Son axe principal est perpendiculaire à la directrice dont on connait la direction ... donc on peut facilement trouver la direction de l'axe principal (qui est axe de symétrie)

Et l'axe principal passe par le foyer (connu) et donc on peut trouver l'équation de l'axe de symétrie.

@Black-Jack Bonjour
comment peut on trouver le sommet et l'axe de symétrie dans ce cas là?
(car je n'ai étudie que les fonction du 2nd degrés)

Pour trouver l'axe de symétrie, j'ai indiqué comment faire.

Il est perpendiculaire à la directrice dont on connait l'équation.

On détermine un vecteur directeur de la directrice.
On en déduit un vecteur directeur de l'axe de symétrie (qui est perpendiculaire à la directrice)

L'axe de symétrie passe par le foyer A :(-1,0).

Avec un vecteur directeur de l'axe de symétrie et un point par lequel il passe ... tu trouves l'équation de l'axe de symétrie.

J'ai oublié de parler du sommet

Quand tu auras trouvé l'équation de l'axe de symétrie ...
il suffira de trouver le point de rencontre de l'axe de symétrie (dont tu auras l'équation) avec la parabole (dont tu connais l'équation)

@Black-Jack la parabole sera de cette forme

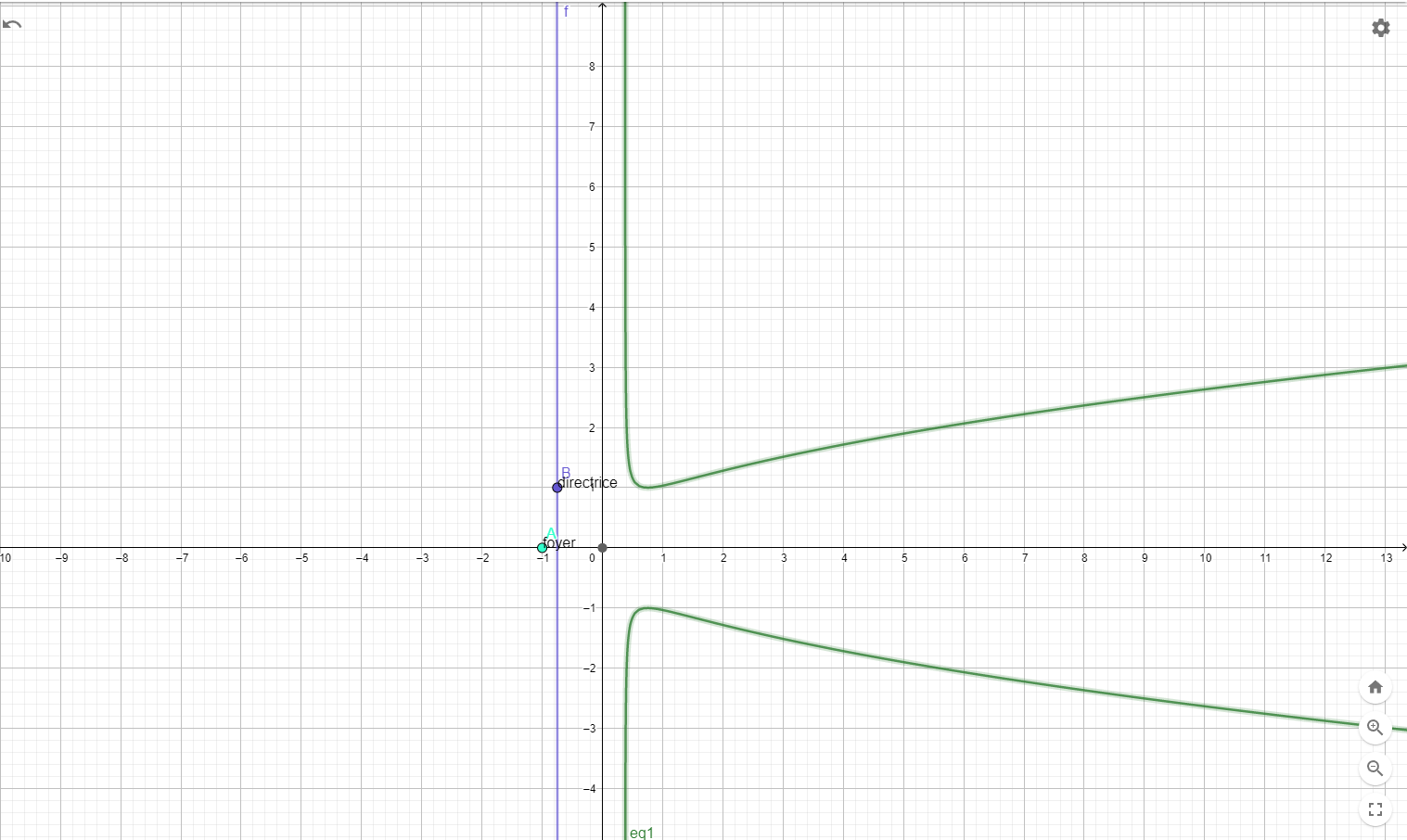
24479d62-7fb1-4e44-8092-8dac459ca86e-2021-11-27 (5).png

@Black-Jack mais je ne sais vraiment pas comment la calculer, donnez moi un indice svp?

Rebonjour

Comme je l'avais dit, je n'avais pas vérifié tes calculs ... j'ai eu tort.

Avec P(X;Y) et A(-1 ; 0), on a = AP² = (X+1)² + Y²

et la distance (au carré) entre P(X;Y) et la directrice est d² = (3X-4Y)²/25

On a donc (X+1)² + Y² = (3X-4Y)²/25

25(X² + 2X + 1 + Y²) = 9X² + 16Y² - 24XY

25X² + 50X + 25 + 25Y² = 9X² + 16Y² - 24XY

16X² + 24XY + 9Y² + 50X + 25 = 0

L'équation de la parabole est : 16x² + 24xy + 9y² + 50x + 25 = 0
A = 16
B = 12
C = 9
AC-B² = 16*9 - 12² = 0 ... c'est bien une parabole.

On peut trouver l'équation de l'axe de symétrie comme je l'ai indiqué.

Et on peut aussi trouver le sommet comme je l'ai indiqué,

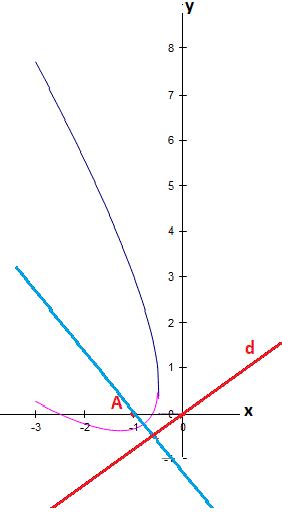
Sans titre.png

@Black-Jack Le sommet a est égale a -3/8

@Black-Jack et l'axe de symétrie est égale à -3/8

directrice : 3x - 4y = 0
y = 3/4 x --> coefficient directeur = 3/4

Les perpendiculaires à la directrice ont un coeff directeur = -1/(3/4) = -4/3
--> y = -4/3 x + k
L'axe de symétrie passe par A(-1 ; 0) -->
0 = 4/3 + k
k = -4/3

L'équation de l'axe de symétrie est donc y = -4/3x - 4/3
soit si on préfère : 4x + 3y + 4 = 0

Et on trouve les coordonnées du sommet, en résolvant le système :

16x² + 24xy + 9y² + 50x + 25 = 0
4x + 3y + 4 = 0

On trouve x = -0,82 et y = -0,24

Sommet : S(-0,82 ; -0,24)

@Black-Jack Merci et bonne soirée

exercices : Distance point-droite

L'équation de la parabole est : 16x² + 24xy + 9y² + 50x + 25 = 0 A = 16 B = 12 C = 9 AC-B² = 16*9 - 12² = 0 ... c'est bien une parabole.

L'équation de la parabole est : 16x² + 24xy + 9y² + 50x + 25 = 0
A = 16
B = 12
C = 9
AC-B² = 16*9 - 12² = 0 ... c'est bien une parabole.