Propriété fonction intégrale limite

Bonjour,
Je bloque sur une question de mon dm de maths qui m’empêche d’avancer, j’aurais besoin d’une piste pour m’aider à trouver la réponse. Soit G(x) = intégrale entre 0 et x de 1/(2 + sin(t))dt

J’ai démontré dans un premier temps que sin t = 2tan(t/2)/(1 + tan^2(t/2))
On me demande par la suite quelle propriété particulière a la fonction G puis en déduire que lim lorsque x tends vers pi- = G(pi). Mais pour l’instant, impossible de trouver la propriété, chose qui a l’air simple mais m’empêche d’avancer.

Merci d’avance pour votre attention.

Bonjour,

sin(t) = 2tan(t/2)/(1+tan²(t/2))

1/(2+sin(t)) = 1/2 * (1 + tan²(t/2))/(1 + tan(t/2) + tan²(t/2))

Poser tan(t/2) = u
1/(2.cos²(t/2))dt = du
avec 1+tan²(t/2) = 1/cos²(t/2) -->
(1+tan²(t/2))/2 dt = du
(1+u²)/2 dt = du
dt = 2/(1+u²) du

1/(2+sin(t)) dt = 1/2 * (1 + tan²(t/2))/(1 + tan(t/2) + tan²(t/2)) dt = (1+u²)/(1 + u + u²) * 2/(1+u²) du

1/(2+sin(t)) dt = du/(1 + u + u²)

S 1/(2+sin(t)) dt = S du/(1 + u + u²) (avec S pour le signe intégral)

S 1/(2+sin(t)) dt = (2/V3) * arctan((2u+1)/V3)

S 1/(2+sin(t)) dt = (2/V3) * arctan((2tan(t/2)+1)/V3)

S(de0àx) 1/(2+sin(t)) dt = (2/V3) * arctan((2tan(t/2)+1)/V3)

S(de0àx) 1/(2+sin(t)) dt = (2/V3) * [arctan((2tan(x/2)+1)/V3) - arctan(1/V3)]

S(de0àx) 1/(2+sin(t)) dt = (2/V3) * [arctan((2tan(x/2)+1)/V3) - Pi/6]

Il y a probablement plus direct.

Zut, j'ai utilisé un changement de variables ... qui, je pense a disparu des programmes de Terminale en France.

Si c'est le cas, il faudra un peu adapter ma réponse.

@Black-Jack merci pour votre réponse, nous avons étudié les changements de variables néanmoins je ne vois toujours pas quelle propriété a la fonction G.

@emilie38 Bonjour,

As-tu étudié la périodicité de la fonction ?

Bonjour,

@emilie38 , j'essaie de comprendre ta question et je la trouve pas claire.
Peut-être faudra-t-il que tu donnes ton énoncé précis pour avoir une réponse précise à ta question.

@emilie38 a dit dans Propriété fonction intégrale limite :

Bonjour,
Je bloque sur une question de mon dm de maths qui m’empêche d’avancer, j’aurais besoin d’une piste pour m’aider à trouver la réponse. Soit G(x) = intégrale entre 0 et x de 1/(2 + sin(t))dt

On me demande par la suite quelle propriété particulière a la fonction G puis en déduire que lim lorsque x tends vers pi- = G(pi).

Voilà ce que je comprends :

$f(t)=12+sintf(t)=\dfrac{1}{2+sint}$

Si ce n'est pas déjà fait, tu peux étudier les variations de cette fonction f , par exemple sur $[−π,π[[-\pi,\pi[$ (c'est à dire sur une période)
Tu trouveras que , sur $[−π,π[[-\pi,\pi[$ , donc sur $R$ , $13≤f(t)≤1\dfrac{1}{3} \le f(t)\le 1$

$G(x)=∫0xf(t)dt\displaystyle G(x)=\int_0^x f(t)dt$

Tu peux justifier que G est continue sur $R$ donc en particulier :

$lim⁡x→π−G(x)=G(π)\displaystyle \lim_{x\to \pi^-} G(x)=G(\pi)$ c'est à dire $lim⁡x→π,x<πG(x)=G(π)\displaystyle \lim_{x\to \pi, x\lt \pi} G(x)=G(\pi)$

@emilie38
Est-ce ça la question ?

Si tu souhaites justifier rigoureusement que G est continue (et non te contenter de le dire) , tu fais une démonstration :
Par exemple :
Tu sais que pour tout $t$ de $R$ , $13<f(t)≤1\dfrac{1}{3}\lt f(t)\le 1$

Soit $x∈Rx\in R$
$G(x+h)−G(x)=∫xx+hf(t)dt\displaystyle G(x+h)-G(x)=\int_x^{x+h}f(t)dt$

$0≤∣G(x+h)−G(x)∣≤∣h∣×max(f(t))0\le |G(x+h)-G(x)|\le |h|\times max(f(t))$

$0≤∣G(x+h)−G(x)∣≤∣h∣×10\le |G(x+h)-G(x)|\le |h|\times 1$

$0≤∣G(x+h)−g(x)∣≤∣h∣0\le |G(x+h)-g(x)|\le |h|$

donc
$lim⁡h→0∣G(x+h)−G(x)∣=0\displaystyle \lim_{h\to 0}|G(x+h)-G(x)|=0$

$lim⁡h→0G(x+h)=G(x)\displaystyle \lim_{h\to 0}G(x+h)=G(x)$

G est continue sur $R$ , en donc en particulier à gauche pour $x=πx=\pi$ , d'où la réponse souhaitée.

Bonjour,

Attention !!!

Il y a une difficulté supplémentaire.

Le fonction f(t) = 1/(2+sin(t)) est continue et donc l'intégrale de f depuis 0 jusque t = x n'a aucune raison de ne pas l'être.

Or comme la fonction tan() est discontinue, il qu'il y a une tan() qui intervient dans (2/V3) * [arctan((2tan(x/2)+1)/V3) - Pi/6],

il y quelque chose de plus à faire.

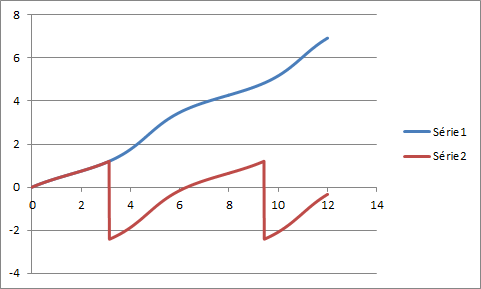
Dit autrement, voici un graphe avec t (donc x) en abscisse et la réprésentation de h(x) = (2/V3) * [arctan((2tan(x/2)+1)/V3) - Pi/6] ainsi que la représentation de la "vraie" intégrale.

Tant que x reste < Pi, les courbes sont identiques ... mais il y a un décalage de Pi+2/V3 au passage à x = Pi, décalage qui va subsister jusque t ou x = 3Pi où le décalage sera double jusque ...

En bleu : la "vraie" intégrale

en brun la fonction h(x) = (2/V3) * [arctan((2tan(x/2)+1)/V3) - Pi/6]

Pour tirer des enseignements sur la "vraie" intégrale, on doit tenir compte de ce que je viens de dire.

La "vraie" intégrale, n'est pas périodique comme semblerait l'indiquer h(x) = (2/V3) * [arctan((2tan(x/2)+1)/V3) - Pi/6]

IL FAUT TENIR COMPTE DES DECALAGES MENTIONNES CI-DESSUS

Sans titre.png

Re-bonjour,

@emilie38 devra préciser sa question (comme déja demandé)

Car si c'est bien la limite à gauche de G en $π\pi$ dont il s'agit, la transformation de sint et le calcul de l'intégrale ne sont pas nécessaires pour répondre à la question qui semble la bloquer...

@emilie38 a d'ailleurs indiqué dans Propriété fonction intégrale limite

@Black-Jack merci pour votre réponse, nous avons étudié les changements de variables néanmoins je ne vois toujours pas quelle propriété a la fonction G.

Il s'agit vraisemblablement de la continuité de la fonction G.