Besoin d’aide exercice maths vecteur seconde
-
Jjedemandeaide dernière édition par jedemandeaide
Bonsoir, j’aurais besoin d’aide pour cet exercice svp.
Soit ABC un triangle. I est le milieu de [AC]: G est le point tel que GA + 2GB + GC = 0 (vecteur nul)
- (a) Montrer que 2GB + GC = -3AG + 2AB + AC
(b) Montrer qu'on a alors AG = 1/2AB + 1/4AC - (a) Faire une figure.
(b) Quelle conjecture peut-on émettre sur la position des points B, G et I? - (a) Exprimer IB en fonction de AB et AC.
(D) alaide de la guestion 1 a) montrer que IG = 1/2AB - 1/4AC
(c) Démontrer la conjecture de la question 2.b)
Je n’ai pas pu mettre les flèches mais tous sont des vecteurs. Merci d’avance.
- (a) Montrer que 2GB + GC = -3AG + 2AB + AC
-
@jedemandeaide Bonsoir,
Indique tes éléments de réponse et la question qui te pose problème.
- Avec la relation de Chasles:
2GB→+GC→=2GA→+2AB→+GA→+AC→=....2\overrightarrow{GB}+\overrightarrow{GC}= 2\overrightarrow{GA}+2\overrightarrow{AB}+\overrightarrow{GA}+\overrightarrow{AC}= ....2GB+GC=2GA+2AB+GA+AC=....
- Avec la relation de Chasles:
-
Jjedemandeaide dernière édition par
@Noemi enfaite j’aimerais juste savoir comment (la démarche à suivre) démontrer que les 2 parties sont égales parce que je n’arrive pas à appliquer la relation de Chasles à -3AG + 2AB + AC.
-
J'ai indiqué le début du calcul pour la question 1 (a) en remplaçant :
GB→=GA→+AB→\overrightarrow{GB}=\overrightarrow{GA}+\overrightarrow{AB}GB=GA+AB et
GC→=GA→+AC→\overrightarrow{GC}=\overrightarrow{GA}+\overrightarrow{AC}GC=GA+AC.Pour la question b) applique la relation de 1 (a) et celle de l'énoncé.
-
Jjedemandeaide dernière édition par
@Noemi j’ai trouvé pour le 1. a) mais j’ai essayé pour le b) j’ai essayé avec AG = AB + BG mais je bloque à 1/2AC + 1/2AC + BA + AC + BG
-
Jjedemandeaide dernière édition par
@jedemandeaide je ne voit pas comment arriver à 1/2AB
-
Pour la question 1 b
GA→+2GB→+GC→=0→\overrightarrow{GA}+2\overrightarrow{GB}+\overrightarrow{GC}= \overrightarrow{0}GA+2GB+GC=0
on déduit:
AG→=2GB→+GC→\overrightarrow{AG}=2\overrightarrow{GB}+\overrightarrow{GC}AG=2GB+GC
or
2GB→+GC→=−3AG→+2AB→+AC→2\overrightarrow{GB}+\overrightarrow{GC}=-3\overrightarrow{AG}+2\overrightarrow{AB}+\overrightarrow{AC}2GB+GC=−3AG+2AB+AC
donc
AG→=−3AG→+2AB→+AC→\overrightarrow{AG}=-3\overrightarrow{AG}+2\overrightarrow{AB}+\overrightarrow{AC}AG=−3AG+2AB+AC
Soit
4AG→=2AB→+AC→4\overrightarrow{AG}=2\overrightarrow{AB}+\overrightarrow{AC}4AG=2AB+AC
D'ou
....
-
Jjedemandeaide dernière édition par
@Noemi et après avoir multiplier par 1/4 2AB et AC on obtient bien AG = 1/2AB + 1/4AC
Merci beaucoup j’avais besoin d’un raisonnement sur lequel me baser.
-
As-tu fait les autres questions ?
-
mtschoon dernière édition par mtschoon

Bonjour,
Illustration graphique : G est le mileu de [IB]
Une justification possible :
GA→+2GB→+GC→=0→\overrightarrow{GA}+2\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}GA+2GB+GC=0
(GA→+GC→)+2GB→=0→(\overrightarrow{GA}+\overrightarrow{GC})+2\overrightarrow{GB}=\overrightarrow{0}(GA+GC)+2GB=0
(GI→+IA→+GI→+IC→)+2GB→=0→(\overrightarrow{GI}+\overrightarrow{IA}+\overrightarrow{GI}+\overrightarrow{IC})+2\overrightarrow{GB}=\overrightarrow{0}(GI+IA+GI+IC)+2GB=0
2GI→+2GB→=0→2\overrightarrow{GI}+2\overrightarrow{GB}=\overrightarrow{0}2GI+2GB=0
GI→+GB→=0→\overrightarrow{GI}+\overrightarrow{GB}=\overrightarrow{0}GI+GB=0
GI→=−GB→\overrightarrow{GI}=-\overrightarrow{GB}GI=−GB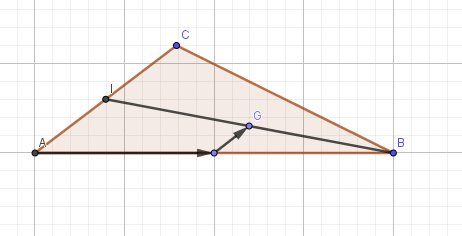
-
Jjedemandeaide dernière édition par
@mtschoon merci beaucoup pour votre aide.
-
Jjedemandeaide dernière édition par
@Noemi bonsoir, je bloque un peu sur la question 3) b). J’ai commencé par IG = IA + AG
= 1/2AB + 2GB + GC
= 1/2AB - 3AG + 2AB + AC
Je ne sais pas si je vais dans le bon sens mais je bloque à partir de là.
Merci d’avance.
-
Jjedemandeaide dernière édition par
@mtschoon bonsoir, ils sont passés où les IA et IC dans la parenthèse dans la 3e ligne. Merci.
-
mtschoon dernière édition par mtschoon

@jedemandeaide , bonsoir,
Je regarde la 3ème ligne et j'explicite la simplification .
I étant le milieu de [AC] :
IA→=−IC→\overrightarrow{IA}=-\overrightarrow{IC}IA=−IC
En transposant :
IA→+IC→=0→\overrightarrow{IA}+\overrightarrow{IC}=\overrightarrow{0}IA+IC=0
donc, la somme IA→+IC→\overrightarrow{IA}+\overrightarrow{IC}IA+IC ne figure donc plus dans l'expression globale.
-
mtschoon dernière édition par

@jedemandeaide , rebonsoir,
Vu que je repasse par là, je regarde.
Tu veux démontrer que IG→=12AB→−14AC→\overrightarrow{IG}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}IG=21AB−41AC ?
Si c'est bien ça :
Comme tu l'as indiqué : IG→=IA→+AG→\overrightarrow{IG}=\overrightarrow{IA}+\overrightarrow{AG}IG=IA+AGTu transformes IA→\overrightarrow{IA}IA :
IA→=12CA→=−12AC→\overrightarrow{IA}=\dfrac{1}{2} \overrightarrow{CA}=- \dfrac{1}{2}\overrightarrow{AC}IA=21CA=−21AC
AG→\overrightarrow{AG}AG a déjà été transformé à la question 1) (b) :
AG→=12AB→+14AC→\overrightarrow{AG}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}AG=21AB+41ACTu déduis en remplaçant les deux vecteurs par les expressions transformées :
IG→=−12AC→+12AB→+14AC→\overrightarrow{IG}=- \dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}IG=−21AC+21AB+41ACTu termines.