lien entre 2 cercles sur un quadrillage 2D (full inconnu)

[zebi7854]

Bonjour,
J'ai besoin d'aide pour savoir quelles positions, 2 traits(noté x.line1.1, y.line1.1 x.line1.2, y.line1.2 et x.line2.1, y.line2.1 x.line2.2, y.line2.2) reliant un premier un rond a un autre, dont on ne connait ni la position(qui sera notée par x.rond1,y.rond1 et x.rond2,y.rond2) ni la taille (notée size1 et size2) sur un quadrillage 2D.
Et bien sur, ce, sans outil de géométrie uniquement par des calculs.

Voici un exemple d'une représentation graphique:

(On cherche donc les valeurs en rouge)

PS: c'est pour du python donc si vous voulez vous pouvez changer le nom des variables

Merci d'avance

[Noemi]

@zebi7854 Bonjour,

Le multipost étant interdit sur ce forum, l'autre post va être supprimé.

Les traits sont tangents aux cercles, donc ...

[mtschoon]

Bonjour,

Si un spécialiste de Python passe par là, peut-être répondra-t-il.

Je ne parle pas de Python, mais de propriétés mathématiques...

@zebi7854 , je te joins un schéma pour éclairer ta question.

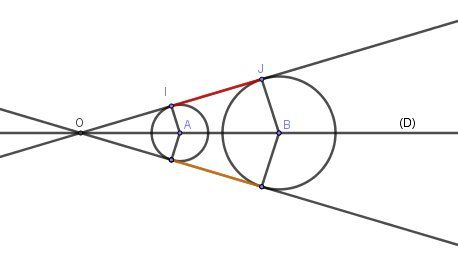
La figure est symétrique par rapport à la droite (D) .

Si c'est la distance $IJ$ que tu cherches, je te donne quelques calculs possibles.

La droite(IJ) est tangente aux cercles.
Toute tangente est perpendiculaire au rayon issu de point de contact.

Le triangles OIA et OJB sont rectangles.
Tu peux apliquer le théorème de Pythagore pour calculer la distanc IJ

$O{I}^2+I{A}^2=O{A}^2$
$O{J}^2+J{B}^2=O{B}^2$

Donc :

$O{I}^2=O{A}^2-I{A}^2$ d'où $OI=\sqrt{O{A}^2-I{A}^2}$
$O{J}^2=O{B}^2-J{B}^2$ d'où $OJ=\sqrt{O{B}^2-J{B}^2}$

$IJ=OJ-OI$ d'où : $\boxed{IJ=\sqrt{O{B}^2-J{B}^2}-\sqrt{O{A}^2-I{A}^2}}$

Si ce sont les tangentes communes extérieures aux deux cercles que tu cherches, , tu peux regarder le document ici :
http://serge.mehl.free.fr/anx/tangente_comm.html

Bons calculs.

[zebi7854]

@mtschoon Donc,
AOI° = asin(AI / AO)
?

[mtschoon]

@zebi7854 ,

Oui, vu que dans le triangle OAI , rectangle en I :
$sin(\widehat{AOI})=\frac{AI}{AO}$

[zebi7854]

Le problème est que l'on ne connait pas la distance OI

[zebi7854]

@zebi7854 Ah nan c'est bon
$AO=\frac{AB}{JB-AI}\ast AI$

[mtschoon]

@zebi7854 ,

Je trouve ta dernière formule écrite très bizarre...

Avec le théorème de Thalès appliqué aux triangles OAI et OBJ (vu que les droites (AI) et (BJ) sont parallèles ), tu peux avoir les proportions:
$\frac{OI}{OJ}=\frac{IA}{JB}=\frac{OA}{OB}$

[zebi7854]

Auriez vous une meilleur solution pour trouver le point $O$ ?

[mtschoon]

@zebi7854 ,

Si tu travailles dans un repère du plan, connaissant les coordonnées de $A,B,I,J$ tu peux trouver des équations des droites $(AB)$ et $(IJ)$ et trouver les coordonnées de leur point d'intersection $O$

[zebi7854]

@mtschoon Sauf que j'ai besoin du point $O$ pour trouver les points $I$ et $J$

[mtschoon]

@zebi7854 ,
Il est difficile de te proposer de l'aide sans vraiment comprendre clairement les données de ton exercice...

Dernière proposition :
http://www.rozenblum.com/tangente-commune-a-deux-cercles/

A tenter...en adaptant les notations
Dans cette proposition de construction géométrique , il est seulement nécessaire de connaître les centres des deux cercles et leurs rayons.

[zebi7854]

Nan mais c'est bon j'ai trouvé comment faire. Il faut juste que je finisse le programme et que je résolve les quelques bugs restants.

En tout cas merci pou votre aide.

[mtschoon]

C'est bien @zebi7854 si ton problème est maintenant solutionné.

Bon courage !

[zebi7854]

Je reviendrai surement lorsque j'aurais fini le programme (Si je n'oublie pas)

[mtschoon]

@zebi7854 , OK
A+, peut-être...
Bonne programmation.

[zebi7854]

@mtschoon Merciiii

[zebi7854]

Ce message a été supprimé !

[zebi7854]

Voici après 2 semaines le programme (pouvant surement être améliorer):

from math import *


def get_angle(x1=0., y1=0., x2=0., y2=0.):
    if y1 - y2 == 0:
        angle = 90
    elif y1 - y2 < 0:
        angle = degrees(atan((x1 - x2) / (y1 - y2)))
    else:
        angle = degrees(atan((x1 - x2) / (y1 - y2))) + 180

    return angle


def turn_a_point(x1=0., y1=0., degre=0., x2=0., y2=0.):
    angle = get_angle(x1, y1, x2, y2)

    x = sin(radians(angle + degre)) * (x1**2 + y1**2)**(1/2)
    y = cos(radians(angle + degre)) * (x1**2 + y1**2)**(1/2)

    return x, y


def lierrond(x1=0., y1=0., size1=0., x2=0., y2=0., size2=0., sizepen=0.):
    angle_from_0 = get_angle(x1, y1, x2, y2)
    xyturned1 = turn_a_point(x1, y1, (90 - angle_from_0))
    xyturned2 = turn_a_point(x2, y2, (90 - angle_from_0))

    xbaseangle = ((size2 * xyturned1[0]) - (size1 * xyturned2[0])) / (size2 - size1)

    angleofthelimit = (degrees(acos((size1/2) / (xbaseangle - xyturned1[0])))) + (180 * ((xyturned1[0] - 
xbaseangle) <= 0))

    dist1 = sqrt(abs(float((size1 / 2)**2) - float((xbaseangle - xyturned1[0])**2)))
    dist2 = sqrt(abs(float((size2 / 2)**2) - float((xbaseangle - xyturned2[0])**2)))

    angle90 = 180 * (angleofthelimit <= 180)

    xlimit1 = sin(radians(180 - angleofthelimit)) * dist1 + xbaseangle + sin(radians(90 - angleofthelimit + angle90)) * sizepen / 2
    ylimit1 = cos(radians(180 - angleofthelimit)) * dist1 + xyturned1[1] + cos(radians(90 - angleofthelimit + angle90)) * sizepen / 2
    xlimit2 = sin(radians(180 - angleofthelimit)) * dist2 + xbaseangle + sin(radians(90 - angleofthelimit + angle90)) * sizepen / 2
    ylimit2 = cos(radians(180 - angleofthelimit)) * dist2 + xyturned1[1] + cos(radians(90 - angleofthelimit + angle90)) * sizepen / 2
    xlimit3 = sin(radians(angleofthelimit)) * dist1 + xbaseangle + sin(radians(90 + angleofthelimit + angle90)) * sizepen / 2
    ylimit3 = cos(radians(angleofthelimit)) * dist1 + xyturned1[1] + cos(radians(90 + angleofthelimit + angle90)) * sizepen / 2
    xlimit4 = sin(radians(angleofthelimit)) * dist2 + xbaseangle + sin(radians(90 + angleofthelimit + angle90)) * sizepen / 2
    ylimit4 = cos(radians(angleofthelimit)) * dist2 + xyturned1[1] + cos(radians(90 + angleofthelimit + angle90)) * sizepen / 2

    xylimit11 = turn_a_point(xlimit1, ylimit1, -90 + angle_from_0)
    xylimit12 = turn_a_point(xlimit2, ylimit2, -90 + angle_from_0)
    xylimit21 = turn_a_point(xlimit3, ylimit3, -90 + angle_from_0)
    xylimit22 = turn_a_point(xlimit4, ylimit4, -90 + angle_from_0)

    return (xylimit11, xylimit12), (xylimit21, xylimit22)

Si qqn pourrait m'aider a le simplifier se serait super