DM sur les vecteurs s'il vous plait c'est urgent

voici l'énoncé:
Soit ABC un triangle où A(11;2), B(3;-2) et C(1,6).
M et N sont les milieux respectifs des côtés [AB]
et [AC]
Soit G défini par GA(vecteur)+GB(vecteur)+GC(vecteur)= 0
Montrer que AG(vecteur)= 1/3AB + 1/3AC.

Pouvez vous m'aider s'il vous plait

@Shiiro Bonsoir (Marque de politesse à ne pas oublier !!)

A partir de $GA→+GB→+GC→=0→\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
Utilise la relation de Chasles :
$GA→+GA→+AB→+GA→+AC→=0→\overrightarrow{GA}+\overrightarrow{GA}+\overrightarrow{AB}+\overrightarrow{GA}+\overrightarrow{AC}=\overrightarrow{0}$
Soit :
$3GA→+AB→+AC→=0→3\overrightarrow{GA}+\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{0}$

Je te laisse poursuivre.

bonsoir, merci beaucoup pour votre aide !

@Shiiro

Tu as terminé l'exercice ?

oui je l'ai terminé il y a quelques minutes

@Shiiro

C'est parfait.
Bonne nuit.

Bonjour,

Visiblement, @Shiiro n'a eu besoin d'aide seulement que pour démontrer que G défini par $GA→+GB→+GC→=0→\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ satisfait à : $AG→=13AB→+13AC→\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}$

Vu qe l'énoncé parle de M et de N, je mets, pour consultation éventuelle, une suite possible :
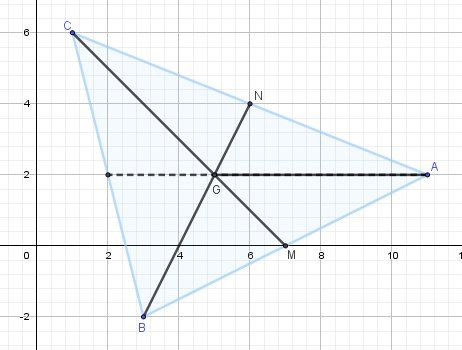
Montrer que le point G (appelé isobarycentre des points A,B,C), est le point d'intersection des médianes c'est à dire le centre de gravité du triangle ABC.

Quelques pistes par calcul vectoriel,

Coordonnées de G
Les coordonnées de $AB→\overrightarrow{AB}$ sont $(3 - 11, - 2 - 2) = (- 8, - 4)$
Les coorconnées de $AC→\overrightarrow{AC}$ sont $(1 - 11, 6 - 2) = (- 10, - 4)$
Les coordonnées de $AG→\overrightarrow{AG}$ sont $x_G-11,y_G-2)$

L'égalité $AG→=13AB→+13AC→\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}$ permet d'écrire:
$xG−11=13(−8)+13(−10)x_G-11=\dfrac{1}{3}(-8)+\dfrac{1}{3}(-10)$ d'où $xG=5\boxed{x_G=5}$
$yG−2=13(−4)+13(4)y_G-2=\dfrac{1}{3}(-4)+\dfrac{1}{3}(4)$ d'où $yG=2\boxed{y_G=2}$

Cordonnées de M et de N
$AM→=12AB→\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}$ permet d'obtenir $M (7, 0)$
$AN→=12AC→\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}$ permet d'obtenir $N (6, 4)$

Alignement des points C,G,M et des points B,G,N
On peut prouver que $CG→=23CM→\overrightarrow{CG}=\dfrac{2}{3}\overrightarrow{CM}$ et $BG→=23BN→\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BN}$

Conclusion
G est le point d'intersection des médianes (CM) et (BN).
Vu que les 3 médianes de tout triangle sont concourantes, G est le point d'intersection des trois médianes donc le centre de gravité du triangle (ABC)

Bonne lecture éventuelle.