Etude d'une fonction du second degré (arc de parabole)

Bonjour je poste ce message car je n'arrive pas à faire la 2ème et 3ème Question de cette exercice suivant

on modélise la trajectoire d'une fusée de feu d'artifice
par un arc de parabole représentée ci-contre. On note h(t) la hauteur
(en mètres) de la fusée en fonction du temps et on a
h(t)= at² + bt + c
La fusée atteint sa hauteur maximale de 80 mètres au bout de 4 secondes
Elle explose 5 secondes après son lancement

que représente ordonnée à l'origine de la courbe ?
2)Déterminer a. b et c
Si la fusée n'avait pas explosé, combien de temps après son lancement serait-elle tombée au sol ( On suppose que la fusée serait tombée à une altitude nulle).

Pour la 1ère Question
J'ai dit que l'ordonnée à l'origine correspond au au début du lancement de la fusée
h(0)=20

Pour la 2éme
j'ai fait la forme canonique qui est= a(t-4)²+ 80
je l'ai développé et j'ai trouver 15/4t²-45/2t-58 ( je pense que c'est faux)
Puis la question 3 je bloque

Voici l'image de la courbe

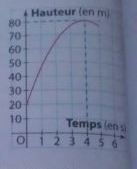
@Rick-Nozi Bonjour,

A partir de la forme canonique et de $h (0) = 20$ , tu détermines la valeur de $a$ .

D'accord j'ai déterminer que a = -15/4

a ( 0 - 4)² + 80 = 20
a x ( -4)² + 80 = 20
16a² + 80 =20
Donc a= -60/16 = -15/4

@Rick-Nozi

Oui,

Donc rectifie le calcul de $h (t)$
$h(t)=−154t2+30t−60+80=...h(t)=-\dfrac{15}{4}t^2+30t-60+80= ...$

h(t)= -15/4 t²+30t +20

Donc a = -15/4

b= 30

c= 20

@Rick-Nozi

C'est correct.
Pour la question 3, résous $h (t) = 0$ .

je trouve des résultat bizarre
x1= (12+8√3)/3

x2= (12 -8 √ 3 ) /3

@Rick-Nozi

C'est correct,
Détermine la valeur qui répond à la question.

j'ai pas compris je peux pas simplifier le calcul plus

@Rick-Nozi

Les résultats sont corrects, cherche la valeur positive.

donc alors c'est x1= (12+8√3)/3

@Rick-Nozi

C'est juste.

Mais j'une Question je n'ai pas compris en quoi ce résultat nous permet de répondre a Si la fusée n'avait pas explosé, combien de temps après son lancement serait-elle tombée au sol ?

@Rick-Nozi

Si on continue le graphique, la courbe décrite est une parabole et on cherche le point qui coupe l'axe des abscisses.

d'accord je vois
Mais juste une chose combien fait x1= (12+8√3)/3 en valeur approchée moi ma calculatrice ne le fait pas

@Rick-Nozi

Tu as quelle calculatrice ?
Le résultat 8,6188...

j'ai une Texas elle ne me pas la forme approchés mais que le résultat juste
En tout Cas Merci pour votre Aide Noemi !!

@Rick-Nozi

Tu peux avoir la valeur approchée en tapant l'expression directement dans la partie calcul.