Produits scalaires 1ère
-
BBubendorf dernière édition par
Bonjour
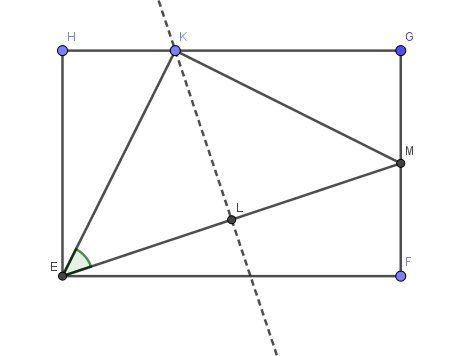
Pouvez vous m'aider avec cet exercice. Je suis en 1ère généraleEFGH un rectangle avec EH=a et EF=3a/2. M le milieu de [FG]et K est défini par vectHK=1/3Vect HG
L est le projeté orthogonal de K sur (EM)
1- Calculer, en fonction de a, les produits scalaires : VectEF x VectEM et VectEH x VectKE
2- En utilisant des relations de Chasles, montrer que VectEK x VectEM = 5a²/4
En exprimant d'une autre façon le produit scalaire Vect EK x xVect EM, en déduire la distance EL en fonction de a
4- Déterminer une mesure en degrés de l'angle KEMMerci par avance
-
@Bubendorf Bonjour,
As-tu fait une figure ?
Indique tes éléments de réponse et la question qui te pose problème.
-
mtschoon dernière édition par mtschoon

Bonjour,
Je te démarre ton exercice si tu as besoin
EF→.EM→=EF→.(EF→+FM→)\overrightarrow{EF}.\overrightarrow{EM}=\overrightarrow{EF}.(\overrightarrow{EF}+\overrightarrow{FM})EF.EM=EF.(EF+FM)
EF→.EM→=EF→.EF→+EF→.FM→\overrightarrow{EF}.\overrightarrow{EM}=\overrightarrow{EF}.\overrightarrow{EF}+\overrightarrow{EF}.\overrightarrow{FM}EF.EM=EF.EF+EF.FMEF→.EF→=(EF→)2\overrightarrow{EF}.\overrightarrow{EF}=(\overrightarrow{EF})^2EF.EF=(EF)2
Tu dois savoir que le carré scalaire d'un vecteur est le carré de sa norme donc :
(EF→)2=(32a)2=94a2(\overrightarrow{EF})^2=(\dfrac{3}{2}a)^2=\dfrac{9}{4}a^2(EF)2=(23a)2=49a2
Si tu préfères, tu peux dire que :
EF→.EF→=EF×EF×cos0=...\overrightarrow{EF}.\overrightarrow{EF}=EF\times EF\times cos 0=...EF.EF=EF×EF×cos0=...
(tu trouveras pareil, bien sûr)EF→.FM→=0\overrightarrow{EF}.\overrightarrow{FM}=0EF.FM=0, vu qu'il s'agit de deux vecteurs orthogonaux.
Si tu préfères, tu peux dire que :
EF→.FM→=EF×FM²²×cosπ2=...\overrightarrow{EF}.\overrightarrow{FM}=EF\times FM²²\times cos\dfrac{\pi}{2}=...EF.FM=EF×FM²²×cos2π=...
(tu trouveras pareil, bien sûr)Conclusion : EF→.EM→=94a2\overrightarrow{EF}.\overrightarrow{EM}=\dfrac{9}{4}a^2EF.EM=49a2
Essaie de poursuivre et reposte si besoin.