Nombre complexe Exercice 3

Bonjour,Pouvez-vous m'aider à resoudre cet exercice svp?
On donne l'expression : 𝐸(𝑧)=𝑧−𝑖 / 𝑧+3 ( 𝑧∈ ℂ)

Déterminer l’ensemble des complexes z tels que E(z) soit un imaginaire pur.
Déterminer l’ensemble des complexes z tels que E(z) soit un réel.
Représenter ces deux ensembles dans le plan de Gauss

@Joyca2 Bonjour,

Cherche l'écriture de la partie réelle et de la partie imaginaire de $E (z)$
en posant $z = x + i y$ .

@Noemi la partie réelle est z/z donc 1 et la partie imaginaire est -i/3 donc E(x) = 1-i/3
Est ce correct ?

@Joyca2

C'est faux.
Ecris $E (z)$ sous la forme $A + B i$
$\dfrac{x+iy-i}{x+iy+3} = ....$

@Noemi ce qui veut dire logiquement que Y vaut 0 ?

@Joyca2
Tu réponds à quelle question ?

@Noemi à la question en faite j'ai pas compris comment vous avez trouver ca? Pouvez-vous détailler svp ?

@Joyca2

J'ai juste suivi les conseils que je te donne. J'ai remplacé $z$ par
$x + i y$ .

Il faut que tu poursuives le calcul et écrire $E (z)$ avec un dénominateur réel.

@Noemi ah ok la je comprend mieux ,je voyais pas au début merci, et pour avoir un deno reel ,je dois remplacer x par un nombre sachant que le deno doit etre different de 0.

@Joyca2

Non,
tu multiplies le numérateur et le dénominateur par le complexe conjugué du dénominateur.

@Noemi ah oui !!! en plus,j'y avais penser !

@Noemi le conjugué du deno c'est x-iy-3 N'est ce pas ? (J'espère ne pas me tromper)

@Joyca2

C'est $x + 3 - i y$

@Noemi si je factorise le deno cela me donne x*2-(iy+3)*2 Est-ce correct ?

@Joyca2

Non,
$x+3+iy)(x+3-iy)= (x+3)^2-(iy)^2=....$

@Noemi ce qui donne (x+3)2+y2 car i*2 vaut -1

@Joyca2

Exact, c'est $x+3)^2+y^2$

Détermine l'expression du numérateur.

@Noemi Desole du retard,voici ce que j'ai trouvé pour le numerateur : x.(x+3)+y.(y-1)-i.(x-3y+3) Est-ce correct ?

je pense que pour que E(z) soit un imaginaire pur x et y doivent etre egale à 0 car lorsque l'on remplace dans l'equation cela nous donne = -i/3 apres simplification !

@Joyca2

C'est correct.
Pour que $E (z)$ soit un imaginaire pur, la partie réelle doit être nulle.

@Noemi et inversement pour que E(z) soit un réelle pur i doit être égale à 0
Pouvez-vous me montrer comment représenter ces 2 ensembles dans le plan de Gauss svp ,je sais vraiment pas ! merci pour votre aide.

@Joyca2

As-tu déterminé les deux ensembles ?

@Noemi Quels 2 ensembles,je vois pas de quel ensemble ? Le domaine?

@Joyca2

Les ensembles sont les réponses aux deux premières questions.

@Noemi ok alors comment les représenter dans un plan de Gauss ?

@Joyca2

Tu représentes la droite et le cercle.

@Noemi donc la droite c'est (x+3)*2+(iy)*2 et le numerateur c'est le cercle c'est ca ?

@Joyca2

Non,

A quelle condition $E (z)$ est un imaginaire pur ?

@Noemi quand la partie réel vaut 0

@Joyca2

Quelle est la partie réelle de $E (z)$ ?

@Noemi c'est x.(x+3)+y.(y-1)/(x+3)°2 + y°2

@Joyca2

Donc il faut déterminer à quel ensemble correspond :
$x (x + 3) + y (y - 1) = 0$

@Noemi L'ensemble que j'ai trouver ce dom appartient à tout les Reels sauf 0,1 et -3
Est-ce correct?

@Joyca2

Non, tu dois trouver l'équation d'un cercle.

@Noemi c'est le denominateur qui ressemble à l'equation d'une Cercle avec (x+3)2 +y2 ce qui me fait penser à x2+y2 = 1

Peut etre que si je distribue x(x+3)+y(y−1)=0 je pourrais mieux apercevoir l'equation du Cercle !

Mais comment la representer ?

@Joyca2

Pour la représentation graphique, il faut déterminer les coordonnées du centre et le rayon.
Ecris $x (x + 3) + y (y - 1) = 0$ sous la forme :
$x-a)^2+(y-b)^2=R^2$

Bonjour,

@Joyca2 , je résume la situation.

si j'ai bien lu, avec les pistes de @Noemi :

$E(z)=(x2+3x+y2−y)+i(3y−3−x)(x+3)2+y2E(z)=\dfrac{(x^2+3x+y^2-y)+i(3y-3-x)}{(x+3)^2+y^2}$

Condition d'existence : $z≠−3z\ne -3$ c'est à dire $(x,y)≠(−3,0)(x,y)\ne (-3,0)$
Le point de coordonnées $(- 3, 0)$ ne peut pas appartenir aux ensembles cherchés

Par contre, pour $z = i$ , $E (z) = 0$ ; vu que $0$ est à la fois réel et imaginaire pur ( $0 = 0 i$ ), le point de coordonnées $(0, 1)$ appartient aux deux ensembles cherchés.

L'ensemble des complexes z tels que E(z) soit imaginaire pur est le cercle d'équation $x^2+3x+y^2-y=0$ , privé du point de coordonnées $(- 3, 0)$
Pour avoir centre et rayon, tu le transformes en
$(x+32)2+(y−12)2=104\biggr(x+\dfrac{3}{2}\biggr)^2+\biggr(y-\dfrac{1}{2}\biggr)^2=\dfrac{10}{4}$
(Vois avec Noemi si tu as besoin d'explication)

L’ensemble des complexes z tels que E(z) soit un réel est la droite d'équation $3 y - 3 - x = 0$ , privée du point de coordonnées $(- 3, 0)$

Bonjour,

@Joyca2 , lorsque tu auras bien compris la méthode algébrique, tu peux regarder la méthode géométrique qui évite tout calcul.

Pour cela, il faut connaître les applications géométriques des nombres complexes.
Cela se traite en Terminale mais j'ignore si tu l'as étudié dans ton cours...

Si tu ne les connais pas, tu ne peux pas les utiliser.

Théorème : $a, b, z$ étant des complexes,
$arg(z−bz−a)=(MA→,MB→)\boxed{arg\biggr(\dfrac{z-b}{z-a}\biggr)=(\overrightarrow{MA},\overrightarrow{MB})}$ ,
avec $z$ affixe de $M$ , $a$ affixe de $A$ et $b$ affixe de $B$ .

Dans ton exercice, tu prends $a = - 3$ et $b = i$
$arg(E(z))=arg(z−iz+3)=(MA→,MB→)\boxed{arg(E(z))=arg\biggr(\dfrac{z-i}{z+3}\biggr)=(\overrightarrow{MA},\overrightarrow{MB})}$

Condition : $z≠−3z\ne -3$ c'est à dire $M≠AM\ne A$

Le point B convient aux deux ensembles

$E (z)$ imaginaire pur <=> $arg(E(z))=+π2arg(E(z))=+\dfrac{\pi}{2}$ ou $−π2-\dfrac{\pi}{2}$ $[2π][2\pi]$
c’est à dire $(MA→,MB→)=+π2(\overrightarrow{MA},\overrightarrow{MB})=+\dfrac{\pi}{2}$ ou $−π2-\dfrac{\pi}{2}$ $[2π][2\pi]$
Le triangle AMB est rectangle en M
L’ensemble des points $M$ est le cercle de diamètre [AB] (privé de A)

$E (z)$ réel <=> $a r g (E (z)) = 0$ ou $π\pi$ $[2π][2\pi]$
c’est à dire $(MA→,MB→)=0(\overrightarrow{MA},\overrightarrow{MB})=0$ ou $π\pi$ $[2π][2\pi]$
Les points $A, M, B$ sont alignés.
L’ensemble des points $M$ est la droite (AB) (privé de A)

Représentation graphique des deux ensembles.
Seuls A, B et I le milieu de [AB] servent à la construction.

Les points $M 1, M 2, M 3, M 4$ sont placés seulement pour illustrer l'explication relative aux angles.
$[2π](\overrightarrow{M_1A}, \overrightarrow{M_1B})=+\dfrac{\pi}{2}\ [2\pi]$
$[2π](\overrightarrow{M_2A}, \overrightarrow{M_2B})=-\dfrac{\pi}{2}\ [2\pi]$
$[2π](\overrightarrow{M_3A}, \overrightarrow{M_3B})=0\ [2\pi]$
$[2π](\overrightarrow{M_4A}, \overrightarrow{M_4B})=\pi\ [2\pi]$

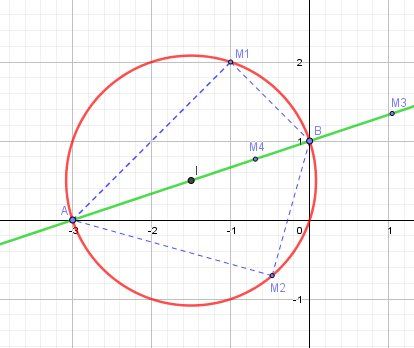
Tu peux t'assurer que les ensembles trouvés par la voie géométrique sont les même que ceux trouvés par la voie algébrique.

Bonne lecture éventuelle.

@mtschoon merci pour ces explication mais je n'est pas encore vue les applications géométriques des nombres complexes. mais j'aimerais savoir comment representer ces 2 ensemble dans le plan de GAUSS svp parce que c'est vraiment le point que je n'arrive pas à faire merci pour votre aide !

@Joyca2

La représentation est donnée par mtschoon. Indique ce que tu ne comprends pas.

@Joyca2 , Bonsoir,

Le Plan de Gauss est le plan que j'appelle tout simplement "Plan complexe"...

Vu que tu as l'équation du cercle , le centre et le rayon , tu ne dois avoir aucun problème.
Remarque : Le centre est I sur le schéma que j'ai joint et le cercle passe par les points A et B .

Vu que tu as l'équation de la droite, tu ne dois avoir aucun problème.
Tu fais les calculs pour avoir 2 points de la droite.
Remarque : cette droite passe par A et B

REMARQUE :
Je te conseille vivement d'écrire l'énoncé que tu as effacé ici :
https://forum.mathforu.com/topic/32574/les-sommes-d-une-suites ...! ! !

@mtschoon je ne pense que vous avez oublier de diviser x°2+3x+y°2−y par (x+3)°2+y°2
non?

@mtschoon Comment vous avez déduit que a : 3/2, b : 1/2 et que le Rayon : 10/4
Pouvez-vous m'expliquer svp (INFOS : J'AI COMPRIS PAR MOI-MEME avec un peu de logique)

@Joyca2 a dit dans Nombre complexe Exercice 3 :

@mtschoon je ne pense que vous avez oublier de diviser x°2+3x+y°2−y par (x+3)°2+y°2
non?

Ma réponse : NON. Aucun oubli...

rappel : une fraction est nulle si et seulement si son numérateur est nul (son dénominateur étant non nul)

Passage par la forme canonique (identités remarquables)

$x2+3x=(x+32)2−94x^2+3x=(x+\dfrac{3}{2})^2-\dfrac{9}{4}$
$y2−y=(y−12)2−14y^2-y=(y-\dfrac{1}{2})^2-\dfrac{1}{4}$

En ajoutant :
$x2+3x+y2−y=(x+32)2+(y−12)2−104x^2+3x+y^2-y=(x+\dfrac{3}{2})^2+(y-\dfrac{1}{2})^2-\dfrac{10}{4}$

Ainsi
$x^2+3x+y^2-y=0$ <=> $(x+32)2+(y−12)2=104(x+\dfrac{3}{2})^2+(y-\dfrac{1}{2})^2=\dfrac{10}{4}$
Regarde la forme générale de l'équation d'un cercle (Noemi te l'a indiqué) et tu déduis le centre et le rayon.

C'est le carré du rayon, c'est à dire $R^2$ , qui vaut $104\dfrac{10}{4}$

La rayon $R$ vaut : $R=102R=\dfrac{\sqrt{10}}{2}$

@mtschoon et son centre est logiquement (a,b) donc (3/2,1/2)

@Joyca2

Non,
Tu as aussi une erreur de signe pour le centre.
Regarde de près ...et réfléchis...

Les coordonnées du centre sont $(−32,12)(-\dfrac{3}{2},\dfrac{1}{2})$

@mtschoon Quand on nous demande de représenter les 2 ensembles cela veut dire que l'on doit tracer la droit d : x-1 (apres simplification) et le Cercle C : (x+3/2)*2+(y-1/2)*2 : 10/4 N'est ce pas ?

@Joyca2 ,

Oui pour le cercle.
Ta simplification pour l'équation de la droite est fausse.

$3 y - 3 - x = 0$ <=> $3 y = x + 3$ <=> $y=13x+1y=\dfrac{1}{3}x+1$