Suite mathématique 1ère
-
hugo.mt_22 dernière édition par Noemi
La suite (u_n) est définie, pour tout entier naturel n, par :
u0=5u_0 = 5u0=5
un+1=7un+5u_{n+1} = 7u_n + 5un+1=7un+5
À partir de quel rang n, a-t-on un≥100u_n ≥100un≥100 ?
-
@hugo-mt_22 Bonsoir, (Marque de politesse une pas oublier !!)
(un)(u_n)(un) est une suite arithmético géométrique.
L'énoncé est-il complet ?
Pas de suite (vn)(v_n)(vn) définie par vn=un+56v_n=u_n+\dfrac{5}{6}vn=un+65 par exemple ?Regarde cette vidéo : https://www.youtube.com/watch?v=6-vFnQ6TghM
Indique tes calculs et/ou résultat si tu souhaites une vérification.
-
mtschoon dernière édition par mtschoon

Bonjour,
@hugo-mt_22 , tu en es peut-être au tout début de ton chapitre sur les suites...
Si c'est le cas , compte les premiers termes.
U0=5U_0=5U0=5
Un+1=7Un+5U_{n+1}=7U_n+5Un+1=7Un+5
Tu remplaces n par 0 : U1=7U0+5=7(5)+5=40U_1=7U_0+5=7(5)+5=40U1=7U0+5=7(5)+5=40
Tu remplaces n par 1 : U2=7U1+5=7(40)+5=285U_2=7U_1+5=7(40)+5=285U2=7U1+5=7(40)+5=285
etc
Si tu continues, avec une calculette par exemple, tu peux trouver:
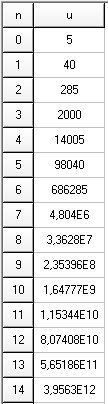
Tu peux donc conjecturer que pour n≥2n\ge 2n≥2 , Un≥100U_n\ge 100Un≥100
Mais cela n'est pas une démonstration mathématique...c'est seulement une conjecture.
Pour faire la démonstration mathématique, tu utilises la piste de Noemi ou bien tu fais une démonstration par récurrence.Tu peux aussi expliquer que la suite est à termes positifs , qu'elle est croissante car Un+1−Un=6Un+5U_{n+1}-U_n=6U_n+5Un+1−Un=6Un+5 d'où Un+1−Un>0U_{n+1}-U_n\gt 0Un+1−Un>0
Comme U2>100U_2\gt 100U2>100, à forciori les termes d'indices supérieurs à 2 seront supérieurs à 100.Peut-être qu'il s'agit seulement une initiation aux suites et dans ce cas, les calculs suffisent et c'est une conjecture qui est demandée...
A toi de voir.