somme de termes d'une suite

Bonjour pouvez vous corriger mon devoir svp?
consigne:
soit un segment [A,B] de longueur r.
Construire le demi-cercle de centre O ou O est le milieu de [A,B] (au dessus de [AB])
Construire le demi-cercle de centre O' ou O' est le milieu de [O,A] (en-dessous de [AB])
Construire le demi-cercle de centre O'' ou O'' est le milieu de [O,O'](au dessus de [AB])
Construire le demi-cercle de centre O''' ou O''' est le milieu de [O',O''] (en dessous de [AB])
….
Calculer I1,I2,I3,.... ,Ii est la longueur de la spirale à l'étape i.
Donner une expression de In en fonction de n.

@Joyca-Le-Boss
pour : I1 j'ai trouver : π.r/2
ensuite I2 : π.r/4
I3 : π.r/8
I4 : π.r/16
c'est une suite géométrique de raison 1/2
Terme général : In = πr/2n

@Joyca-Le-Boss , bonjour,

Schéma (si j'ai bien compris)

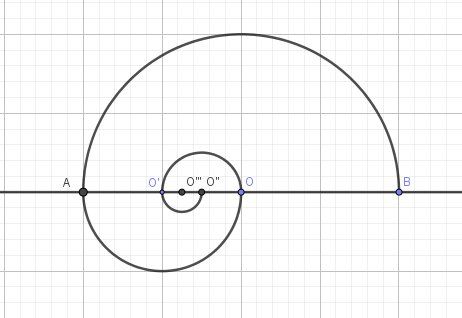
Ce que tu as calculé, c'est le périmètre de chaque demi-cercle, ce n'est pas la longueur de la spirale ; il faut ajouter ces périmètres

Effectivement, ces périmètres que j'appelle $p_1,p_2,...,p_n,...$ forment une suite géométrique de raison $12\dfrac{1}{2}$

$p1=πr(12)p_1=\pi r(\dfrac{1}{2})$
De façon générale $pn=πr(12)np_n=\pi r(\dfrac{1}{2})^n$

Mais, $l_n$ est la longueur de la spirale.

$l_n=p_1+p_2+...+p_n$

Pour l'expression de $l_n$ applique la formule de la somme des n premiers termes de la suite géométrique de premier terme $p_1$ et de raison $12\dfrac{1}{2}$

@mtschoon
Et donc expressions de In
=> In= p1.1-1/2*n/1-1/2
Merci, j'avais confondu aire et périmètre mais j'ai compris mon erreur!

@Joyca-Le-Boss

Simplifie l'expression indiquée.

@Noemi alors => 1/2*n/1/2

@Joyca-Le-Boss

Non, vérifie le calcul et soigne l'écriture du résultat.

Bonsoir,

@Joyca-Le-Boss a dit dans somme de termes d'une suite :

@mtschoon
Et donc expressions de In
=> In= p1.1-1/2*n/1-1/2
Merci, j'avais confondu aire et périmètre mais j'ai compris mon erreur!

@Joyca-Le-Boss , à regarder de très près, ta formule est exacte mais très mal écrite

Je crois lire :
$ln=p1×1−(12)n1−12l_n=p_1\times \dfrac{1-(\dfrac{1}{2})^n}{1-\dfrac{1}{2}}$

Si c'est ça, remplace $p_1$ par sa valeur et simplifie.

@Joyca-Le-Boss ,

ça doit donner, au final :
$ln=πr(1−(12)n)l_n=\pi r\biggr(1-(\dfrac{1}{2})^n\biggr)$