Géométrie dans l'espace et orthogonalité
-
YYuri123453 dernière édition par Noemi
Bonjour, pouvez-vous m'aider avec l'exercice suivant:
L'énoncé est le suivant : SABC un tétraèdre. Au plan de quelle face le point M tel que vecAM+3vecMB+vecAC= vect nul appartient-il ?
Le démontrer.Ici j'ai dit qu'on avait donc (tout est en vecteur):
AM+MB+2MB+AC=0
AB+AC+2MB=0
BM=1/2AB+1/2AC
Mais je ne sais pas comment continuer ni comment le démontrer, peut etre avce une fugure?
-
@Yuri123453 Bonjour,
A quel plan appartient le vecteur AB→+AC→\overrightarrow{AB}+\overrightarrow{AC}AB+AC ?
le point BBB ?
d'ou ...
-
YYuri123453 dernière édition par
Le vecteur AB+AC ainsi que le point B appartiennent au plan (ABC)
Donc le point M appartient au plan M
-
Rectifie la dernière phrase.
-
YYuri123453 dernière édition par
oh oui désolé. Donc le point M appartient au plan (ABC)
-
YYuri123453 dernière édition par
De plus je devais cela à l'oral, est-ce que vous auriez des explications plus précise ou complète ou vous penser que je peux l'expliquer assez facilement avec ce que j'ai ici
-
Tu peux éventuellement faire une figure.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Yuri123453 , je regarde ton énoncé :
@Yuri123453 a dit dans Géométrie dans l'espace et orthogonalité :
Bonjour, pouvez-vous m'aider avec l'exercice suivant:
L'énoncé est le suivant : SABC un tétraèdre. Au plan de quelle face le point M tel que vecAM+3vecMB+vecAC= vect nul appartient-il ?
Le démontrer.Ici j'ai dit qu'on avait donc (tout est en vecteur):
AM+MB+2MB+AC=0
AB+AC+2MB=0
BM=1/2AB+1/2AC
Mais je ne sais pas comment continuer ni comment le démontrer, peut etre avce une fugure?@Yuri123453 , pour compléter les réponses prcédentes, je te propose une construction possible de M dans le plan (ABC)
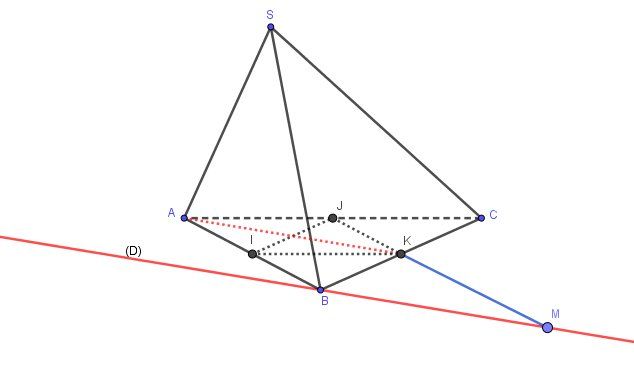
Soit I,J,KI,J,KI,J,K les milieux respectifs des segments [AB],[AC],[BC][AB],[AC],[BC][AB],[AC],[BC].AB→+AC→=AK→+KB→+AK→+KC→=2AK→\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AK}+\overrightarrow{KB}+\overrightarrow{AK}+\overrightarrow{KC}=2\overrightarrow{AK}AB+AC=AK+KB+AK+KC=2AK
Donc, BM→=AK→\boxed{\overrightarrow{BM}=\overrightarrow{AK}}BM=AK
La quadrilatère AKMBAKMBAKMB est un parallélogramme.
M est donc sur la droite (D) passant par B et parallèle à (AK)
De plus, (KM)//(AB)(KM)//(AB)(KM)//(AB)
Vu que (JK)//(AB)(JK)//(AB)(JK)//(AB) comme droite des milieux du triangle ABCABCABC, les points J,K,MJ,K,MJ,K,M sont alignés.Conclusion :
M est le point d'intersection de la droite (D) avec la droite (JK).
-
YYuri123453 dernière édition par
D'accord merci beaucoup pour votre aide!
-
mtschoon dernière édition par

De rien @Yuri123453 et bon oral !
-
Zzoela dernière édition par
@Noemi
bonjour, il appartierent au plan ABC
-
mtschoon dernière édition par

@zoela , bonjour,
Oui, effectivement, cela a été expliqué .