fonctions Reciproques Ex 2

Bonsoir,Pouvez-vous m'aider à resoudre cet exercice ? svp
𝑓(𝑥)=𝑥³−𝑥°2+3
En déduire trois abscisses ayant même image.

@Joyca2 Bonsoir,

Etudie les variations de la fonction $f$ .

@Noemi je dois faire sa derivé premiere ?

@Joyca2

Oui.

@Noemi je les fait ensuite que faut -il faire?

@Joyca2

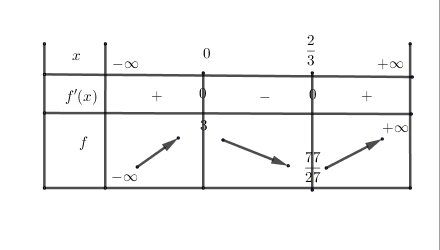
Etudie le signe de la dérivée et dresse le tableau de variations.

@Noemi je les dresser mais il me faut les zeros de f(x) que j'ai pas su trouver mais j'ai trouver les zeros de sa derivé qui est x = 0 et x=2/3

@Joyca2

Il faut analyser le tableau de variations.
As-tu calculé les limites.

Bonjour,

@Joyca2 a terminé son exercice seul ou bien il l'a abandonné...

Quelques pistes pour consultation événtuelle.
$f(x)=x^3-x^2+3$
$f'(x)=3x^2-2x=x(3x-2)$

Tableau de variation
$f (0) = 3$ et $f(23)=7727f(\dfrac{2}{3})=\dfrac{77}{27}$ d'où $f(23)≈2.85f(\dfrac{2}{3})\approx 2.85$

Représentation graphique

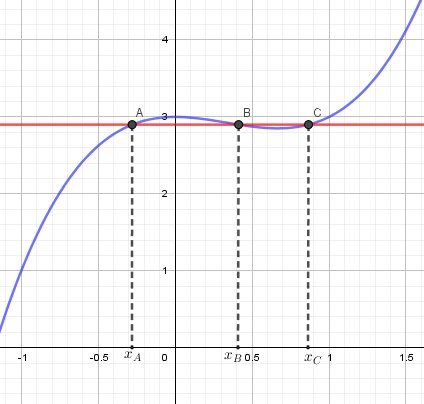
En choissant une valeur de y comprise entre $7727\dfrac{77}{27}$ et $3$ , par exemple $y = 2.9$ , la droite d'équation $y = 2.9$ ( en rouge) coupe la réprésentation graphique de f (en bleu) en trois points $A, B, C$ , d'abscisses respectives $x_A,x_B,x_C$

Donc $x_A,x_B,x_C$ ont la même image $2.9$ par f.

Si une conclusion était demandée, on pourait dire que f n'est pas une application injective de $R$ vers $R$ .

Bonne lecture éventuelle.