Etudier une fonction
-
Prince Of Darkness dernière édition par Prince Of Darkness
Bonjour,
J'ai cet exercice a resoudre.- soit f la fonction définie sur l'intervalle [1 ;25] par : f(x)= (x+2-ln(x)) /x
a) démontrer que f'(x)=(-3+ln(x)) /x^2 (fait)
b) résoudre dans [1 ;25] inéquation -3+ln(x) > 0 (j'ai trouvé x>e^3)
c) dresser le tableau de variation de la fonction sur [1 ;25]
d) démontrer que dans [1 ;25] équation f(x)=1.5 admet une seule solution
e) determiner un encadrement d'amplitude 0.01 de alpha
La question c'est, est-ce que je dois trouver les limites de cette fonction et si oui, est-ce que c'est toujours quand x tend vers - l'infi et + l'infi.
Merci d'avance.
- soit f la fonction définie sur l'intervalle [1 ;25] par : f(x)= (x+2-ln(x)) /x
-
@Prince-Of-Darkness Bonjour,
La fonction est définie sur l'intervalle [1;25], donc pour le tableau de variations, tu dois calculer f(1)f(1)f(1) et f(25)f(25)f(25).
-
Prince Of Darkness dernière édition par
Et pour la question d il faut que j'utilise la tvi normale ou monotone svp?
-
Utilise le résultat du tableau de variations et le TVI.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Prince-Of-Darkness , pour vérification éventuelle,
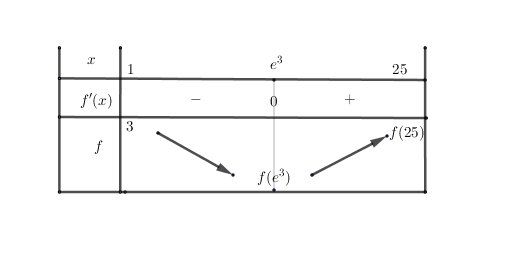
f(25)=27−ln(25)25f(25)=\dfrac{27-ln(25)}{25}f(25)=2527−ln(25) d'où f(25)≈0.95124f(25)\approx 0.95124f(25)≈0.95124
f(e3)=e3−1e3f(e^3)=\dfrac{e^3-1}{e^3}f(e3)=e3e3−1 d'où f(e3)≈0.95021f(e^3)\approx 0.95021f(e3)≈0.95021
Sur [e3,25][e^3,25][e3,25], l'équation f(x)=1.5f(x)=1.5f(x)=1.5 n'a pas de solution.
Sur [1,e3][1,e^3][1,e3], tu utilises le TVI (cas de la bijection)
1.5∈[f(e3),3]1.5\in[f(e^3),3]1.5∈[f(e3),3]
Il existe une valeur unique α\alphaα de [1,e3][1,e^3][1,e3] telle de f(α)=1.5f(\alpha)=1.5f(α)=1.5α\alphaα est donc le solution unique de l'équation f(x)=1.5f(x)=1.5f(x)=1.5 sur [1,25][1,25][1,25]
A la calculette 2.31<α<2.322.31\lt \alpha\lt 2.322.31<α<2.32
Bonne lecture éventuelle.