TRIGONOMETRIE dm maths

Bonjour, je n'arrive pas à la question 2 et 3 pourriez vous m'expliquer svp.
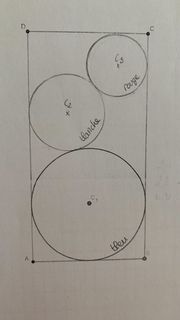
On considère un cylindre en verre dans lequel on introduit trois boules de couleurs différentes.
Elles son empilées pour formé un élément décoratif.
La boule la plus grosse, de 12 cm de diamètre, bleue, est déposé au font. On admet qu'elle y glisse
sans jeu avec les bords.
La seconde, blanche, de 8 cm de diamètre, ce cale en reposant sur celle déjà introduite et en
s'appuyant sur un bord du cylindre (à gauche par exemple quand l'objet est devant soit).
La dernière, rouge, de 6 cm de diamètre, se cale en reposant sur la blanche et en s'appuyant sur
le bord opposé.

Analyser le texte pour :
a.
Corriger en rouge les fautes de français sur ce document
b. Compléter le dessin ci-dessous pour illustrer complètement la situation.
Déterminer la hauteur exacte de l'empilement des boules dans le cylindre pour pouvoir
placer un couvercle. (Une étude mathématique basée sur la géométrie est évidemment
attendue).
Si on appelle C1 C2 et C3 les trois centres des boules dans l'ordre d'introduction,
déterminer l'angle C2C1C3

@Cécilia-Bourgeois Bonsoir,

As-tu complété le dessin ? placé les centres des boules, la distance à calculer.
Utilise le dessin illustrant la situation et décompose la hauteur à calculer.

donc pour la hauteur je pensais ajouter tous les diamètres mais ca ne va pas

Ce message a été supprimé !

@Noemi

@Cécilia-Bourgeois , bonjour,

Les rayons sont plus adaptés mais il y a d'autres longueurs à calculer !

Je te joins un schéma (les mesures sont totalement approximatives !)

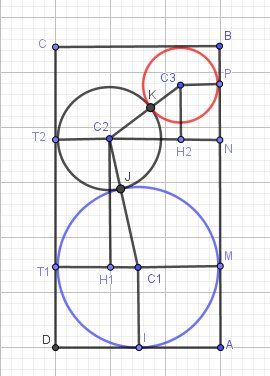
Je te mets quelques indications pour la question 2)
Il faudra que tu donnes des jutifications géométriques (centres des cercles alignés aves le point de contact des cercles)

Je te mets quelques indications pour la question 2)

Tu dois calculer BC=BM+MN+NP+PC

$BM=C_1M=6$ (rayon)
$PC=C_3P=3$ (rayon)

Je te donne une indication pour calculer MN
$MN=H_1C_2$
Tu peux appliquer le théorème de Pythagore dans le triangle $H_1C_1C_2$ rectangle en $H_1$

$C_1C_2)^2=(H_1C_2)^2+(H_1C_1)^2$

$H_1C_1=T_1C_1-T_2C_2=6-4=2$
$C_1C_2=C_1J+jC_2=6+4=10$

Tu peux ainsi déduire $H_1C_2)^2$ , pui $H_1C_2$ c’est à dire $M N$

Pour calculer $N P$ , tu appliques la même méthode en utilisant le triangle rectangle $C_2H_2C_3$ rectangle en $H_2$

Remarque :

Les notations dans l'ordre que tu indiques pour les sommets du rectangle dans ton schéma (que tu as envoyé pendant que je tapais ma réponse) ne sont aps celles de mon schéma , mais c'etait seulement un changement de notations (pour les sommets du rectangle).
La hauteur correspondant au rayon du grand cercle est 6
La hauteur correspondant au rayon du petit cercle est 3
Les calculs de MN et NP ne changent pas.

@mtschoon merci beaucoup je reviens vers vous si besoin pour les angles

@Cécilia-Bourgeois ,d'accord, mais tu peux donner les valeurs des longueurs si tu souhaites une vérification car elles te seront nécessaires pour les calculs d'angles.

alors j'ai trouvé AM = 6 MN = 4racine de 6 NP = 2racine de 6 PB = 3
donc AB= 9+6racinede6

cependant pour l'angle je comptait faire

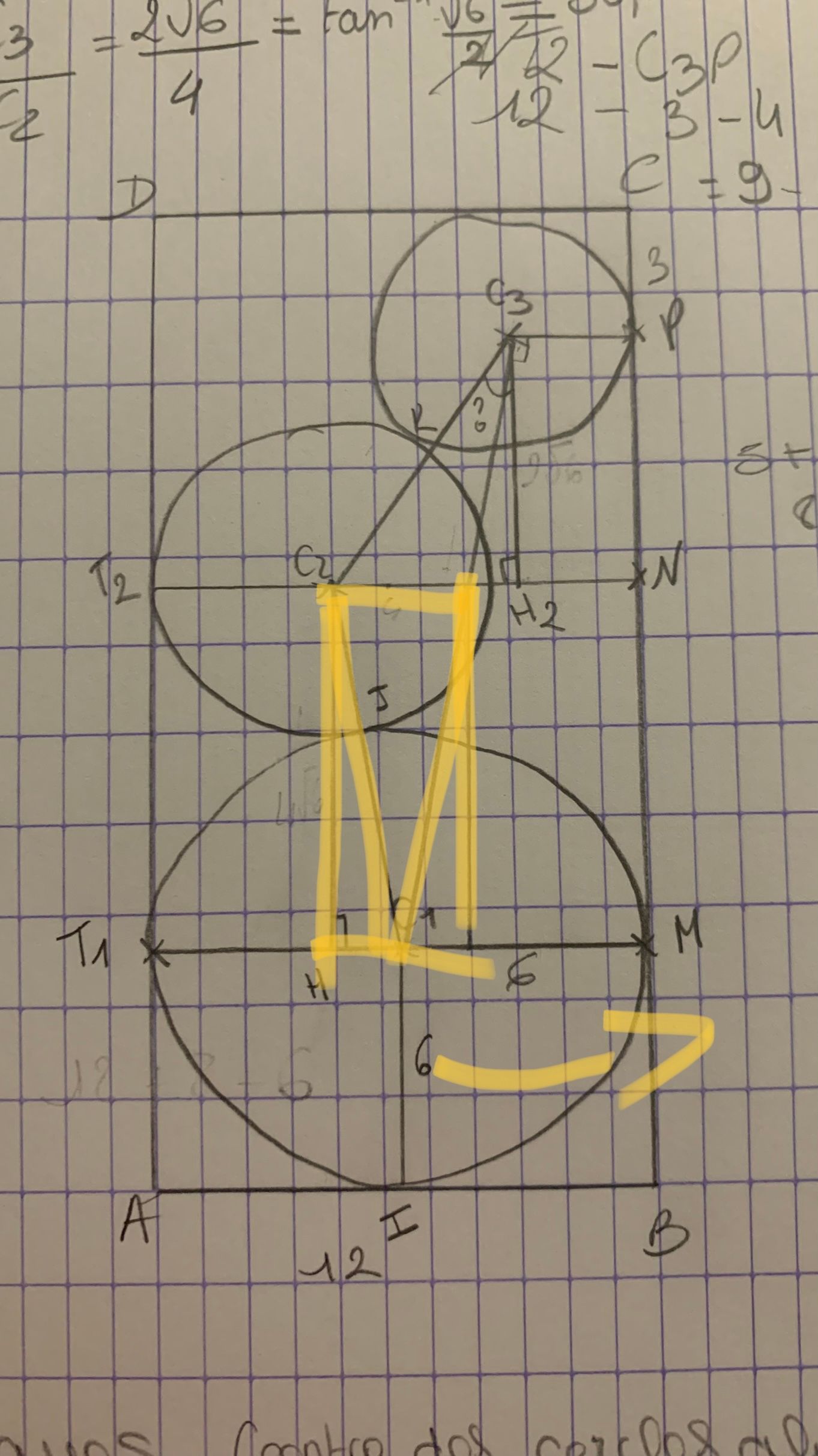
@Cécilia-Bourgeois

Pour le calcul de l'angle, utilise la trigonométrie dans un triangle rectangle.

@Noemi mais le problème c'est que mon triangle n'est pas rectangle

@Cécilia-Bourgeois

Tu décomposes l'angle en deux.
Calcule l'angle $C_3C_2H_2$ puis l'angle $H_2C_2C_1$

@Noemi d’accord merci mais est ce que mon résultat est juste au moins ? de la hauteur ?

@Noemi mais après le problème c'est que l'hypoténuse du triangle qu'on cherche ne passe pas par H2

@Cécilia-Bourgeois

J'ai utilisé ton schéma pour indiquer les angles à calculer.
Si tu utilises l'autre schéma précise le.
Dans ce cas tes résultats sont justes : $A M = 6$ , $MN=46MN=4\sqrt6$ et $2\sqrt6$ , ....
Les angles à calculer : $C_3C_2H_2$ et $H_2C_2C_1$
Remarque les angles $H_2C_2C_1$ et $C_2C_1H_1$ sont égaux car ....

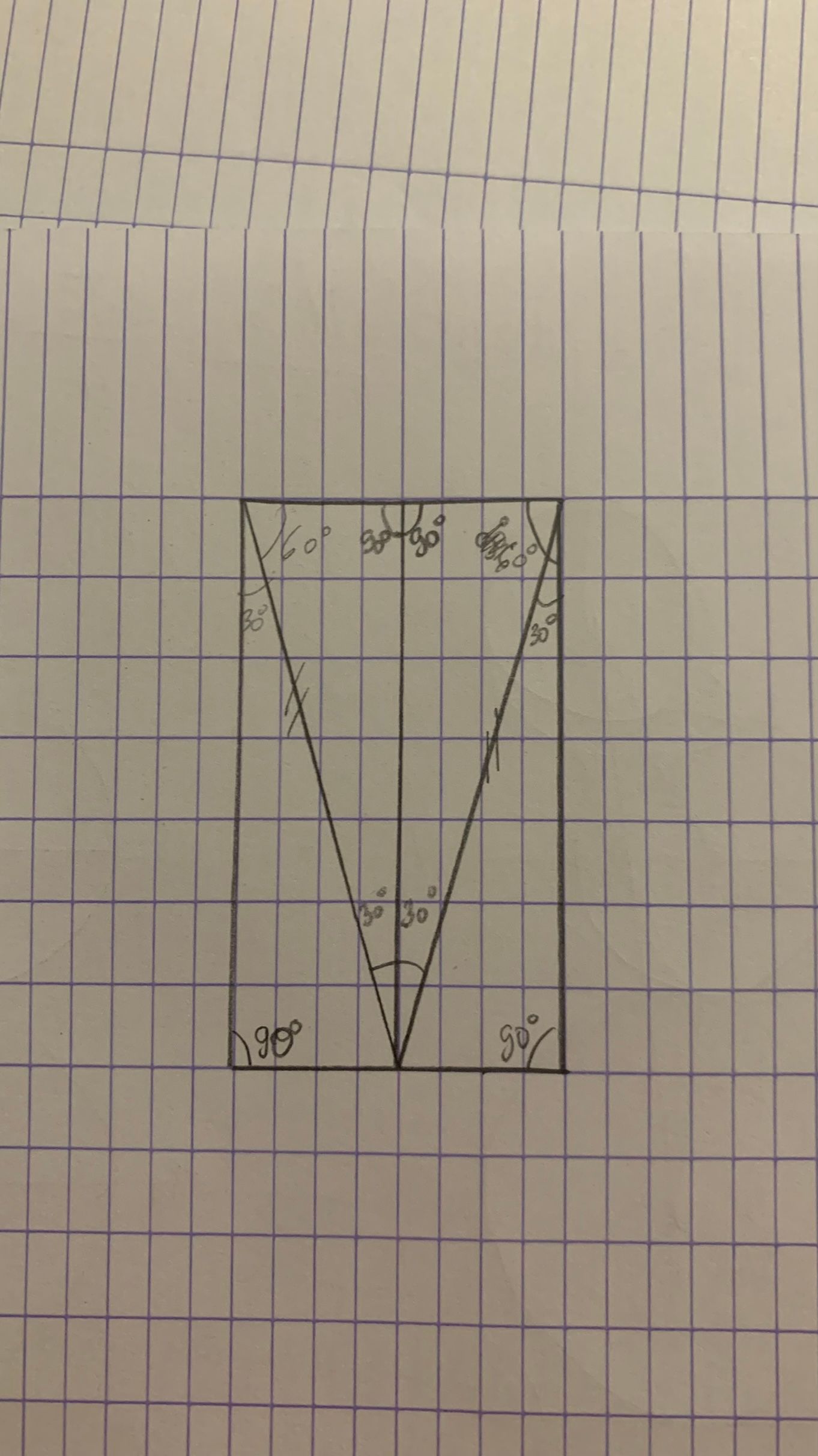
donc si j'ai bien compris les angles à calculer sont les suivant
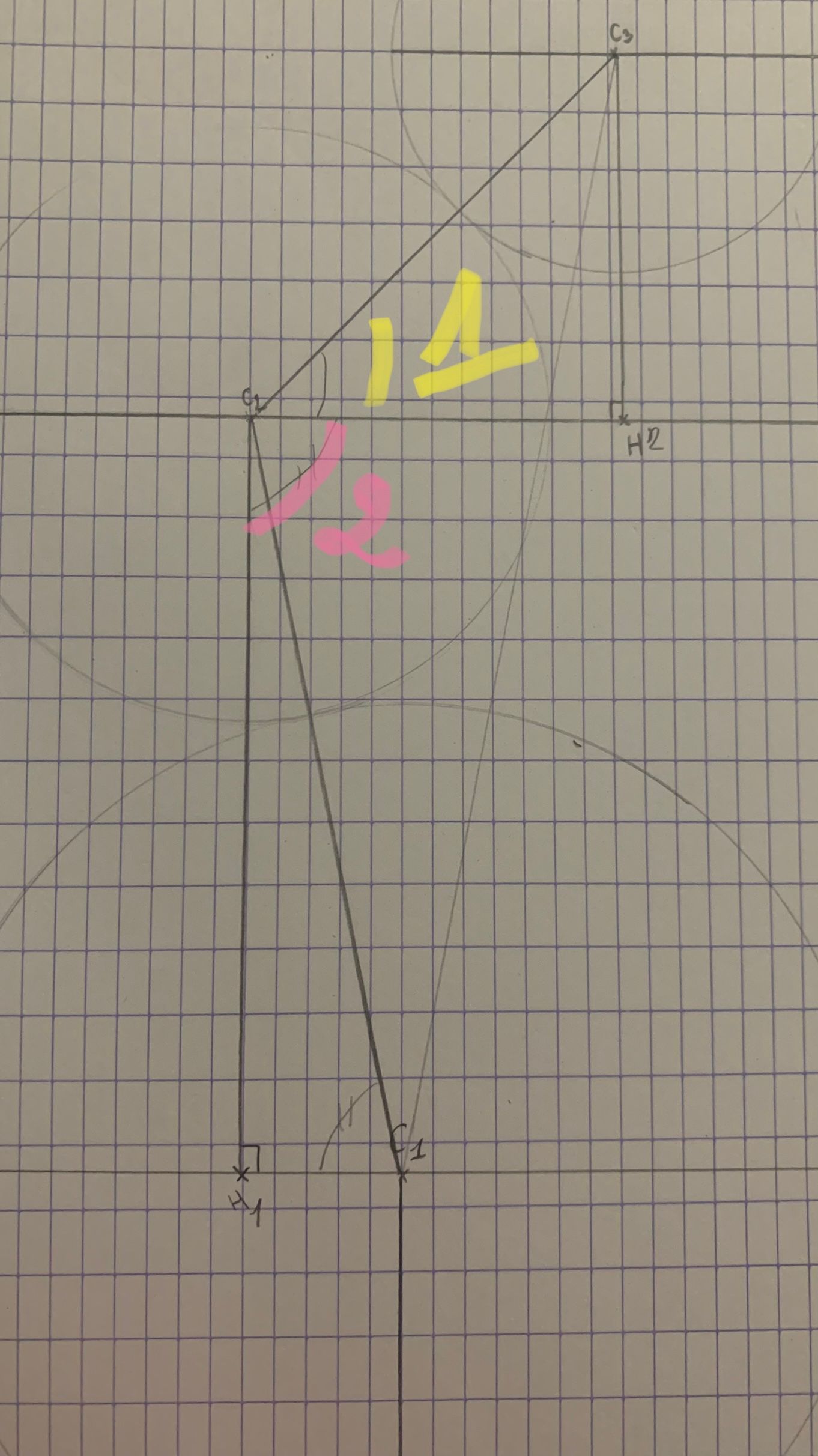
Et les angles H2C2C1 et C2C1H1 sont égaux car si je forme un rectangle (voir image suivant)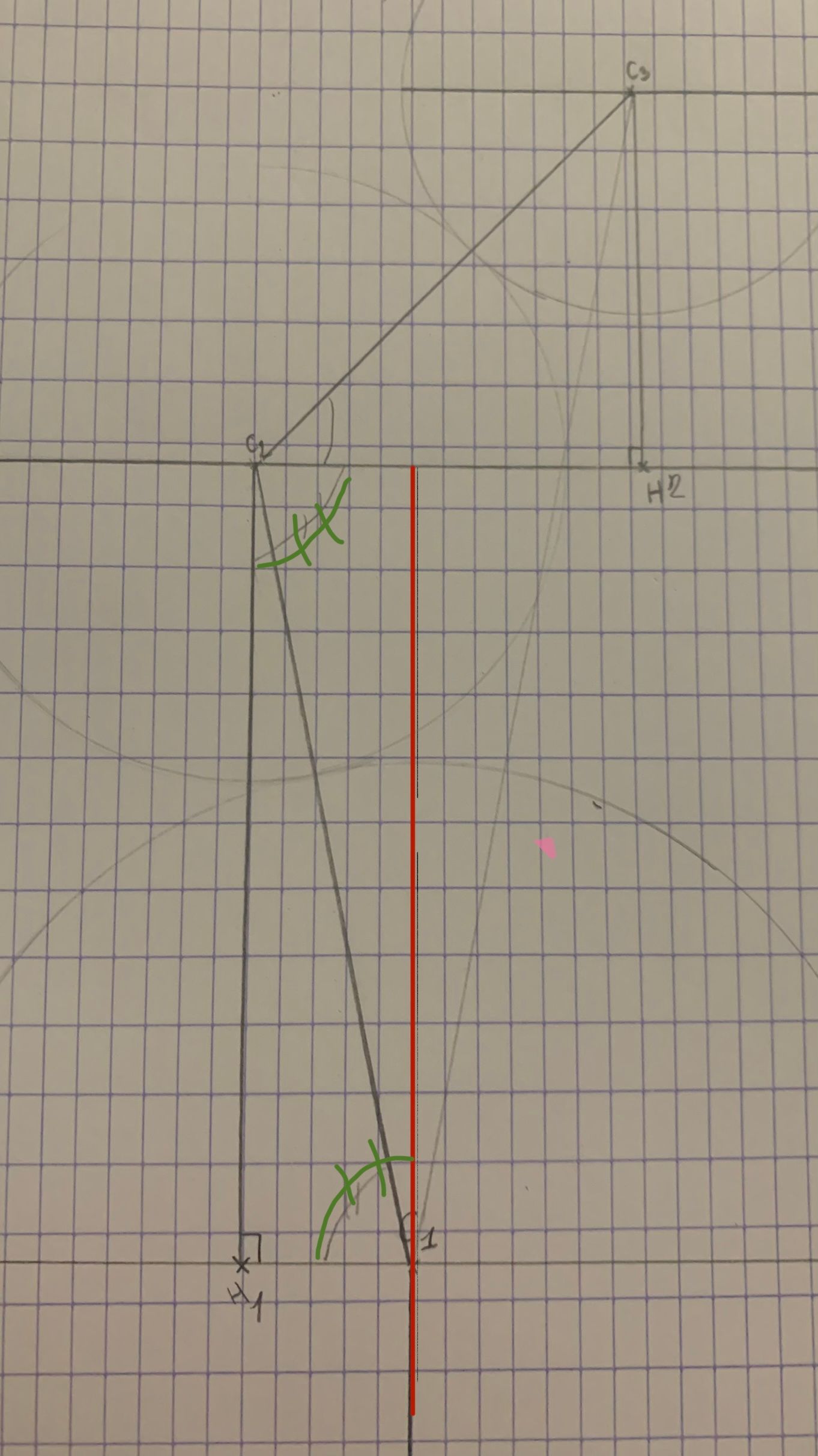 et après comment je fais pour diviser l'angle avec le trait C1C2

@Cécilia-Bourgeois

Le deuxième angle marqué n'est pas bon.

Alors je pense avoir trouvé: j'ai calculé l'angle C3C2H2: cos-1 5/7= 44,41°
ensuite j'ai calculé l'angle H2C2C1: sin-1 5/10= 60°
Et vue que H2C2C1 et HC1C2 sont égaux puisque que si on transltate le triangle sur symétrie de l'hypoténuse nous obtenons un rectangle et alors les angles sont égaux. Donc HC1C2= 30°. A mettons je crée le point Q permettant de faire le rectangle alors HC1Q forme un angle droit et vue que nous savons que les angles sont complémentaire alors si HC1C2=60° alors C2C1Q= 30° et étant donné que Q coupe en 2 l'angle C2C1H2 alors on le multiplie par deux et l'angle C2C1H2= 15x2= 30°;

...... PFFFFF J'AI L'IMPRESSION DE RIEN COMPRENDRE

@Cécilia-Bourgeois

Vérifie le calcul pour l'angle $H_2C_2C_1$ .

Donc oui je me suis trompé j'aurais du faire le cos-1 5/10= 60° donc l'angle H2C2C1=60°

@Noemi Et donc si H2C2C1=60° alors C2C1H1=60° aussi avec la regle du rectangle mais alors comment trouvé l'angle qui manque ? car si on fait l'histoire de complémentarité cela voudrait dire que la moitié de l'angle C1=30° pour finir les 90° de l'angle droit du rectangle et donc si on fait x2 cela veut dire que l'angle C2C1H2=60° mais je trouve cela élevé

@Cécilia-Bourgeois

Non
$H_1C_1=2$ et $C_1C_2=10$
donc....

@Noemi alors cos-1 2/10= 78,46°
mais du coup H2C2C1 différent de C2C1H1.
Je ne comprend pas vous aviez dit qu'il était égaux

@Noemi Alors il y a quelque chose qui m'échappe pourquoi quand on fait H2C2C1 on obtient un angle plus petit (cos-1 5/10) que si on fait cos-1 2/10 alors qu'on calcul le même angle

@Cécilia-Bourgeois

Le triangle $H_2C_2C_1$ n'est pas un triangle rectangle donc tu ne peux utiliser les relations du triangle rectangle.
C'est pour cela que tu calcules l'angle $C_2C_1H_1$ car le triangle correspondant est rectangle.
Tu dois justifier que les angles $H_2C_2C_1$ et $C_2C_1H_1$ sont égaux.

Ah oui que je suis bête et petit question à quoi nous a servi de calculer l'Angle C3C2H2 ?

Et donc après nous faisons 90-78,46 = 11,54 --> donc ça ce n'est que la moitié de l'angle C2C1C3 et après on multiplie par 2 non ?

@Noemi et c'est comme avoir calculer l'angle C2 on me le demande pas alors pourquoi l'avoir calculer?

@Cécilia-Bourgeois

Tu dois calculer l'angle $C3C2C1^\widehat{C_3C_2C_1}$ et
l'angle $C3C2C1^=C3C2H2^+H2C2C1^\widehat{C_3C_2C_1}= \widehat{C_3C_2H_2}+\widehat{H_2C_2C_1}$

@Noemi non je devais calculer seulement C2C1C3

@Noemi MERCI BQ DE TON AIDE VRAIMENT

@Cécilia-Bourgeois

J'ai mal lu l'énoncé, je pensais que c'était l'angle $C1C2C3^\widehat{C_1C_2C_3}$ qu'il fallait calculer.
Pour l'angle $C2C1C3^\widehat{C_2C_1C_3}$ utilise les relations trigonométriques pour un triangle quelconque.

Bonjour,

@Cécilia-Bourgeois ,

Pour la question 2), je confirme ce que tu as trouvé pour la hauteur exacte de l'empilement des boules et que t'a déjà confirmé @Noemi :
$MN=46MN=4\sqrt 6$
$NP=26NP=2\sqrt 6$
Hauteur totale cherchée : $9+669+6\sqrt 6$

Pour la question 3)
Tout dépend des relations trigonométriques que tu connais.

Tu peux, comme déjà indiqué, utiliser une relation métrique dans un triangle quelconque (de la forme $cosA^a^2=b^2+c^2-2bc\ cos\widehat{A}$ )

En l'appliquant au triangle $C_2C_1C_3$ , tu dois trouver, après calculs, que $cos(C2C1C3^)=276300=2325cos(\widehat {C_2C_1C_3})=\dfrac{276}{300}=\dfrac{23}{25}$

d'où, à la calculette, avec la fonction $cos^{-1}$

$C2C1C3^≈23,07°\boxed{\widehat {C_2C_1C_3}\approx 23,07°}$ (sauf erreur)

Sinon, tu peux aussi utiliser les deux triangles rectangles situés de part et d'autre de l'angle $C2C1C3^\widehat {C_2C_1C_3}$

Dans le triangle $C_2H_1C_1$ : $tanH1C1C2^=H1C2H1C1=26tan\widehat {H_1C_1C_2}=\dfrac{H_1C_2}{H_1C_1}=2\sqrt 6$
d'où, à la calculette, avec la fonction $tan^{-1}$ , tu trouves $H1C1C2^\widehat {H_1C_1C_2}$

Dans le triangle $C_1H_3C_3$ : $tanH3C1C3^=H3C3H3C1tan\widehat {H_3C_1C_3}=\dfrac{H_3C_3}{H_3C_1}$
d'où, à la calculette, avec la fonction $tan^{-1}$ , tu trouves $H3C1C3^\widehat {H_3C_1C_3}$

Conséquence :
$C2C1C3^=180°−(H1C1C2^+H3C1C3^)\widehat {C_2C_1C_3}=180°-(\widehat {H_1C_1C_2}+\widehat {H_3C_1C_3})$

Tu trouveras pareil qu'avec la méthode précédente (je viens de faire la vérification) :
$C2C1C3^≈23,07°\boxed{\widehat {C_2C_1C_3}\approx 23,07°}$

Bons calculs !