Bonjour, j'aimerais avoir de l'aide sur l'énoncer suivant :

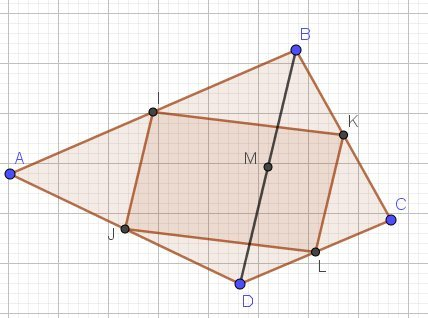
on munit le plan du repère (A ; vecteur AD ; vecteur AB) et note (x;y) les coordonnées du point C. question 1 : Déterminer les coordonnées des autres points de la figure en fonction de x et y si nécessaire. question 2 calculer les coordonnées des vecteurs IJ et KL.

@Améthyste Bonjour,

Quelles sont les coordonnées des points A, D et B?
Comment sont placés les points I, K, J, L, et M ?

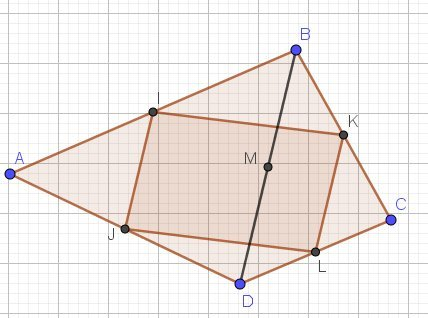
Les coordonnées de A ; D ; et B je ne suis pas sur mais est-ce que c'est IJ pour A; IJ pour B IK; et D JL

I,J,L,K forme un parallélogramme est M coupe le parallélogramme

@Améthyste

L'énoncé est-il complet ?
Le plan est muni du repère : $(A;AD→;AB→)(A;\overrightarrow{AD};\overrightarrow{AB})$
donc $A (0; 0)$ , $D (1; 0)$ , $B (0; 1)$ .

oui l'énoncer est complet, j'aimerais savoir comment avait vous trouver ses resultats

@Améthyste

Ces résultats sont donnés par la définition d'un repère.
La figure est donnée dans l'énoncé ?

Bonjour,

@Améthyste , ton dessin est très bien mais ton énoncé n'est vraiment pas clair...

Je tente de t'expliquer ce que sont les coordonnées de $A, D, B$

Dans un repère usuel, les axes de coordonnées sont souvent perpendiculaires (on parle de repère orthogonal) et même parfois, en plus, les vecteurs unitaires ont même "longueur" (je devrais dire même "norme") ; on parle de repère orthonormé).

Ici, ce n'est pas le cas.

L'origine des axes est le point A (qui de façon usuelle s'appelle O).
Donc $A$ a pour coordonnées $(0, 0)$

L'axe des abscisses est la droite orientée $(A D)$ et le vecteur unitaire (qui de façon usuelle s'appelle $i→\overrightarrow{i}$ ), ici est le vecteur $AD→\overrightarrow{AD}$
Donc $D$ est le point de l'axe des abscisses qui a pour abscisse 1.
Tout point de l'axe des abscisses a pour ordonnée 0 donc $D$ a pour coordonnées $(1, 0)$

L'axe des ordonnées est la droite orientée $(A B)$ et le vecteur unitaire (qui de façon usuelle s'appelle $j→\overrightarrow{j}$ ), ici est le vecteur $AB→\overrightarrow{AB}$
Donc $B$ est le point de l'axe des ordonnées qui a pour ordonnée 1.
Tout point de l'axe des ordonnées a pour abscisse 0 donc $B$ a pour coordonnées $(0, 1)$

Réflechis à tout ça.

@Améthyste , j'invente un énoncé...
J'ignore si c'est le bon...
Soit C(x,y)
I,J,K,L étant les milieux respectifs de [AB],[AD][BC],[CD] , déterminer les coordonnées de ces points I,J,K,L
Déterminer les coordonnées de $IJ→\overrightarrow{IJ}$ et de $KL→\overrightarrow{KL}$
En déduire la narure du quadrilatère ILJK

Tu as, dans ton cours, les formules pour trouver les coordonnées du milieu d'un segment.
Tu l'appliques aux 4 segments.
I milieu de [AB]
$xI=xA+xB2x_I=\dfrac{x_A+x_B }{2}$
$yI=yA+yB2y_I=\dfrac{y_A+y_B }{2}$
Tu dois trouver $I(0,12)I(0,\dfrac{1}{2})$

J milieu de [AD]
Tu dois trouver $I(12,0)I(\dfrac{1}{2},0)$ Calculs à faire

K milieu de [BC]
Tu dois trouver $I(x2,1+y2)I(\dfrac{x}{2},\dfrac{1+y}{2})$ Calculs à faire

L milieu de [CD]
Tu dois trouver $L(1+x2,y2)L(\dfrac{1+x}{2},\dfrac{y}{2})$ Calculs à faire

Conséquence pour les vecteurs :

$IJ→\overrightarrow{IJ}$ a pour coordonnées $(xJ−xI,yJ−yJ)=(12,−12)(x_J-x_I, y_J-y_J)=(\dfrac{1}{2},-\dfrac{1}{2})$ Calculs à faire

$KL→\overrightarrow{KL}$ a pour coordonnées $(xL−xK,yL−yK)=(12,−12)(x_L-x_K, y_L-y_K)=(\dfrac{1}{2},-\dfrac{1}{2})$ Calculs à faire

Conclusion : les vecteurs $IJ→\overrightarrow{IJ}$ et $KL→\overrightarrow{KL}$ étant égaux, le quadrilatère IJLK est un prallélogramme.

M semble être le milieu de [BD]
On peut calculer ses coordonnées ( $12,12)\dfrac{1}{2},\dfrac{1}{2})$ mais je ne vois pas l'intérêt...

Bons calculs @Améthyste pour le cas où l'énoncé indiqué est le bon .
Comme indiqué, aucun calcul n'ai fait dans ma réponse.