Exercice sur les suites

[mik16]

Bonjour, j'aurai besoin d'aide pour cet exercice :
*Le but de cet exercice est de calculer des termes de la suite ($U_n$) définie par :
$U_n$ = 0² + 1² + 2² + ... + n²
pour tout 𝑛 ≥ 0

1. Calculer $U_0$ ,$U_1$, $U_2$, $U_3$.
2. Justifier que cette suite est croissante strictement.
3. Créer un script Python qu’on recopiera sur la copie permettant d’obtenir la valeur de $U_n$ en fonction d’une valeur 𝑛 demandée à l’utilisateur en début de script. (avec définition d’une fonction ou non). Obtenir la valeur de $U_{100}$ à partir du script.
4. Déterminer un polynôme 𝑃 de degré 3 vérifiant, pour tout 𝑛 ≥ 0 : 𝑃(𝑛 + 1) − 𝑃(𝑛) = 𝑛².
5. Exprimer $U_{100}$ à l’aide de valeurs issues du polynôme 𝑃. Retrouver la valeur obtenue au 3).*

Merci d'avance pour votre aide.

[Noemi]

@mik16 Bonjour,

Indique tes éléments de réponse et la question qui te pose problème.

[mtschoon]

Bonjour,

@mik16 , je regarde ton énoncé,

@mik16 a dit dans Exercice sur les suites :

Bonjour, j'aurai besoin d'aide pour cet exercice :
*Le but de cet exercice est de calculer des termes de la suite ($U_n$) définie par :
$U_n$ = 0² + 1² + 2² + ... + n²
pour tout 𝑛 ≥ 0

1. Calculer $U_0$ ,$U_1$, $U_2$, $U_3$.
2. Justifier que cette suite est croissante strictement.
3. Créer un script Python qu’on recopiera sur la copie permettant d’obtenir la valeur de $U_n$ en fonction d’une valeur 𝑛 demandée à l’utilisateur en début de script. (avec définition d’une fonction ou non). Obtenir la valeur de $U_{100}$ à partir du script.
4. Déterminer un polynôme 𝑃 de degré 3 vérifiant, pour tout 𝑛 ≥ 0 : 𝑃(𝑛 + 1) − 𝑃(𝑛) = 𝑛².
5. Exprimer $U_{100}$ à l’aide de valeurs issues du polynôme 𝑃. Retrouver la valeur obtenue au 3).*

@mik16 , voici quelques pistes pour démarrer,

$U_n=0^2+1^2+2^2+...+n^2$

Tu ne dois pas avoir de difficultés pour calculer les premiers termes
$U_0=0^2=0$
$U_1=0^2+1^2=1$
etc

Pour trouver le sens de variation de la suite, tu calcules le signe de $U_{n+1}-U_n$, pour tout $n$ de $N$
$U_{n+1}-U_n=(0^2+1^2+2^2+...+n^2+(n+1{)}^2)-(0^2+1^2+2^2+...+n^2)$
Après simplification, il reste :
$U_{n+1}-U_n=(n+1{)}^2$
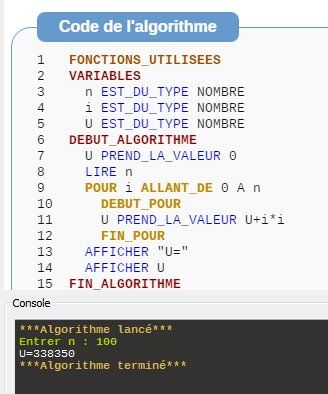
Vu que $(n+1{)}^2>0$, tu tires la conclusion.

Pour l'algorithme permettant d’obtenir la valeur de $U_n$ en fonction d’une valeur $n$ demandée à l’utilisateur en début de script, je te joins un algorithme en langage naturel ( fait avec Algobox), car je n'utilise pas Python.

Tu le consultes et lorsque tu as compris, tu le traduis en Python (boucle FOR)
Remarque :
$i\ast i$ peut s'écrire bien sûr $i^2$ (je n'ai pas utilisé la puissance 2 car Algobox a une écriture assez particulière pour les puissances)

Tu dois trouver : $U_{100}=338350$

Etudie tout ça de près et essaye de continuer.

[mtschoon]

@mik16 , je te mets quelques pistes pour la suite,
Je ne te fais pas les calculs, je te donne simplement des pistes.

A la question 4), tu cherches un polynôme $P(x)$ de la forme
$P(x)=a{x}^3+b{x}^2+cx+d$

$P(n+1)-P(n)=n^2$ c'est à dire
$a(n+1{)}^3+b(n+1{)}^2+c(n+1)+d-a{n}^3-b{n}^2-cn-d=n^2$

Après calculs(identités remarquables), simplifications et regroupements, tu dois obtenir :
$3a{n}^2+n(3a+2b)+a+b+c=n^2$

Par identification pour tout $n$ de $N$:
$\{\begin{array}{l}3a=1\\ 3a+2b=0\\ a+b+c=0\end{array}$

Après calculs, $a=\frac{1}{3}$, $b=-\frac{1}{2}$, $c=\frac{1}{6}$
$d$ est quelconque.
Le plus simple est de prendre $d=0$
$\boxed{P(x)=\frac{1}{3}{x}^3-\frac{1}{2}{x}^2+\frac{1}{6}x}$

La 5) est la conséquence pour calculer $U_{100}$ d'une autre façon.

Tu utilises la propriété $P(n+1)-P(n)=n^2$ pour $n$ allant de $100$ à $0$ :

$\{\begin{array}{l}P(101)-P(100)=100^2\\ P(100)-P(99)=99^2\\ P(99)-P(98)=98^2\\ ...\\ ...\\ ...\\ P(2)-P(1)=1^2\\ P(1)-P(0)=0^2\end{array}$

Tu ajoutes membre à membre ces égalités :
A gauche, "presque" tout se simplifie
Il reste :
$P(101)-P(0)=100^2+99^2+99^2+...+1^2+0^2$
c'est à dire , vu que $P(0)=0$
$P(101)=100^2+99^2+99^2+...+1^2+0^2$

Je te laisse terminer et tu dois retrouver la valeur de $U(100)$ obtenue avec l'algorithme.

Bons calculs.
Reposte si besoin.

[mik16]

D'accord merci beaucoup pour votre aide,
bonne journée.

[mtschoon]

De rien @mik16 .
J'espère que tu es arrivé à tout traiter dans cet exercice.