Dérivation d’un quotient

Bonjour, j’ai des difficultés à dériver ce quotidien est ce que quelqu’un pour m’aider ?
$f(x)=2(x2+ax+1)x2+2x+5f(x)=\dfrac{2(x^2+ax+1)}{x^2+2x+5}$
Jai du mal à dévirer ce quotient.

@myriam Bonjour,

Domaine de définition ?
Indique tes calculs :
$u(x) =2(x^2+ax+1)$ : $u^{'} (x) = . . . .$
$v(x) =x^2+2x+5$ : $v^{'} (x) = . . . . .$

Bonjour,

Bizarre...

@mya ( ou @myriam) car myriam vient de devenir mya ...? ?) , tu as plusieurs pseudos ? et tu as le même exercice que @ada ?

https://forum.mathforu.com/topic/32713/partie-calcul-littéral-d-un-exercice-de-dérivation

Si s'agit du même exercice (ce qui semble totalement être le cas), il aurait fallu rester sur le topic initial...

@Noemi jai braucoup de mal à comprendre la démarche

@myriam

Complète les pointillés
$u^{'} (x) = . . . .$
$v^{'} (x) = . . . .$

Puis tu appliques la formule :
$(UV)′=U′V−UV′V2(\dfrac{U}{V})'=\dfrac{U'V-UV'}{V^2}$

@Noemi
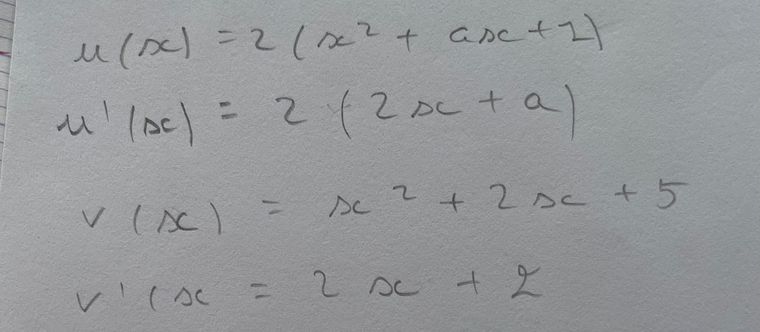la première etape est correcte ?

@mya

C'est juste.
Remplace chaque termes par son expression dans la formule de la dérivée puis développe et simplifie le numérateur.

@Noemi jai trouver le meme résultat que dans l’énonçé mon calcul final est donc correct merci de votre aide !

@mya

C'est parfait.

Bonjour,

mya ( c'est à dire myriam ou ada ?) n'a pas eu de difficulté pour vérifier son résultat , car, en fait, il était dans l'aide à ada (dans la discussion ouverte ave le pseudo "ada"..)

Je trouve dérangeant ces mélanges de peudos ...

En consultant les adresses IP, on doit pouvoir avoir une petite idée ...