Trigonométrie 1ére générale
-
hugo.mt_22 dernière édition par
Bonjour,
Quel est l'ensemble des solutions sur [0;2π[ de
−√3/2≤cos(x)<1/2
-
mtschoon dernière édition par

@hugo-mt_22 , re-bonjour,
Revois les angles remarquables, si besoin.
cos(π3)=12cos(\dfrac{\pi}{3})=\dfrac{1}{2}cos(3π)=21
cos(5π6)=−32cos(\dfrac{5\pi}{6})=-\dfrac{\sqrt 3}{2}cos(65π)=−23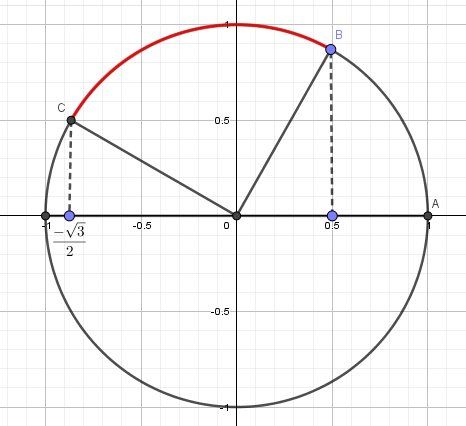
Tu tires la conclusion.
-
hugo.mt_22 dernière édition par
Bonjour,
Cela est égal à pi/3; pi/2; 2pi/3; 3pi/4; 5pi/6 ?
-
@hugo-mt_22 Bonjour,
L'ensemble solution est un intervalle. x∈]....]x \in ] .... ]x∈]....]
-
mtschoon dernière édition par

@hugo-mt_22 , réfléchis à l'arc de cercle en rouge sur le schéma fait.
-
hugo.mt_22 dernière édition par
Bonjour,
Cela donne ]pi/3; pi/2[U]pi/3; pi/2;]
-
Bizarre cette réponse, tu écris deux fois à π2\dfrac{\pi}{2}2π inclus ou non, le même intervalle !
-
hugo.mt_22 dernière édition par
Je ne comprend pas.
Serait il possible de me donner la réponse pour que cela puisse m'aider à visualiser pour la prochaine fois?
-
A partir du cercle trigonométrique, quelle est la mesure de l'angle AOB ?
-
hugo.mt_22 dernière édition par
Il mesure 60°
-
Oui 60° ou π3\dfrac{\pi}{3}3π radians et l'angle AOC ?
-
hugo.mt_22 dernière édition par
@Noemi Il mesure 150°
-
mtschoon dernière édition par

Bonjour,
@hugo-mt_22 , parle en radians!
(OA→,OB→)=π3(\overrightarrow{OA},\overrightarrow{OB})=\dfrac{\pi}{3}(OA,OB)=3π [2π][2\pi][2π]
(OA→,OC→)=5π3(\overrightarrow{OA},\overrightarrow{OC})=\dfrac{5\pi}{3}(OA,OC)=35π [2π][2\pi][2π]
-
mtschoon dernière édition par mtschoon

Désolée, je n'avais pas vu les derniers posts...
Je n'avais vu que la réponse en degrés de @hugo-mt_22
-
hugo.mt_22 dernière édition par
[5π/6; 5π/6[U]10π/6;14π/6]
-
Oui, 150° ou 5π6\dfrac{5\pi}{6}65π donc l'intervalle ....
-
hugo.mt_22 dernière édition par
Je sais pas
-
Donc
x∈ ]π3:5π6]U[....;....[x \in \ ] \dfrac{\pi}{3}:\dfrac{5\pi}{6}] U[ .... ; ....[ x∈ ]3π:65π]U[....;....[
-
hugo.mt_22 dernière édition par
-5π/6 et -π/3
-
hugo.mt_22 dernière édition par
Je pense que c'est cela.
-
Comme xxx appartient à [0;2π[[0; 2\pi[[0;2π[
x∈ ]π3;5π6]U[7π6;5π3[x \in \ ] \dfrac{\pi}{3};\dfrac{5\pi}{6}] U[\dfrac{7\pi}{6}; \dfrac{5\pi}{3}[ x∈ ]3π;65π]U[67π;35π[
-
mtschoon dernière édition par mtschoon

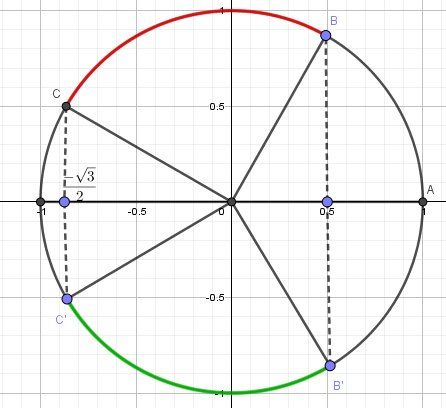
Schéma complet, si besoin.