vecteurs de l'espace

[ASMAE]

BONJOUR J'ai besoin d'aide

𝑺𝒐𝒊𝒕 𝑺𝑨𝑩𝑪𝑫 𝒖𝒏𝒆 𝒑𝒚𝒓𝒂𝒎𝒊𝒅𝒆 𝒅𝒆 𝒃𝒂𝒔𝒆
𝒖𝒏 𝒑𝒂𝒓𝒂𝒍𝒍è𝒍𝒐𝒈𝒓𝒂𝒎𝒎𝒆 𝑨𝑩𝑪𝑫 ;𝒍𝒆𝒔 𝒑𝒐𝒊𝒏𝒕𝒔
𝑰 ; 𝑱 𝒆𝒕 𝑲 𝒓𝒆𝒔𝒑𝒆𝒄𝒕𝒊𝒇𝒔 𝒍𝒆𝒔 𝒎𝒊𝒍𝒊𝒆𝒖𝒙 𝒅𝒆 [𝑺𝑩]
𝑺𝑪⃗+ 𝑩𝑫⃗= 𝑺𝑫⃗ + 𝑩𝑪⃗= 𝟐𝑰𝑱⃗
𝑺𝑫⃗+ 𝑩𝑨⃗= 𝑺𝑨⃗ + 𝑩𝑫⃗=𝟐𝑰𝑲⃗

[Noemi]

@ASMAE Bonjour,

Indique tes éléments de réponse.
Quelle est la question ?

[ASMAE]

@Noemi
Montrer les les égalités

[Noemi]

@ASMAE

Comment sont placés les points J et K ?

[mtschoon]

Bonjour,

@ASMAE , si tu ne donnes pas l'énoncé total, on ne peut guère t'aider...
Il faut indiquer où sont les points I,J,K.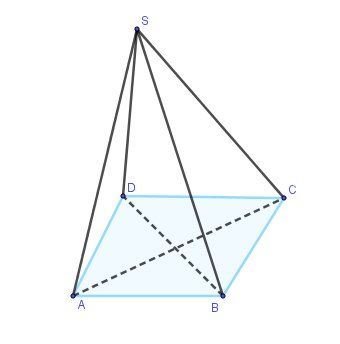

Avec la relation de Chasles, tu peux prouver les deux égalités de gauche (de tes doubles égalités)
$\overrightarrow{SC}+\overrightarrow{BD}=(\overrightarrow{SD}+\overrightarrow{DC})+(\overrightarrow{BC}+\overrightarrow{CD})$

Tu peux supprimer les parenthèses et regrouper à ta guise (associativité de l'addition vectorielle)
$\overrightarrow{SC}+\overrightarrow{BD}=(\overrightarrow{SD}+\overrightarrow{BC})+(\overrightarrow{DC}+\overrightarrow{CD})$

$(\overrightarrow{DC}+\overrightarrow{CD})=\overrightarrow{0}$ vu qu'il s'agit de la somme de deux vecteurs opposés.

Donc : $\boxed{\overrightarrow{SC}+\overrightarrow{BD}=\overrightarrow{SD}+\overrightarrow{BC}}$

Tu pratiques de la même façon pour la somme $\overrightarrow{SD}+\overrightarrow{BA}$
$\overrightarrow{SD}+\overrightarrow{BA}=(\overrightarrow{SA}+\overrightarrow{AD})+(\overrightarrow{BD}+\overrightarrow{DA})$
$\overrightarrow{SD}+\overrightarrow{BA}$=....Tu regroupes de la même façon et tu trouves la réponse voulue.

Si tu as besoin de plus d'aide, complète ton énoncé.