Trigonométrie 1ère maths
-
hugo.mt_22 dernière édition par
Bonjour,
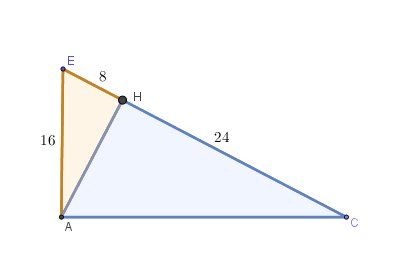
EAC est un triangle et HH est le pied de la hauteur issue de AA.
EH =8
CH = 24CH=24
EA = 16EA=16Calculer EA→⋅AC→:
Calculer CE→⋅CA→:
Calculer EH→⋅EA→:
-
BBlack-Jack dernière édition par
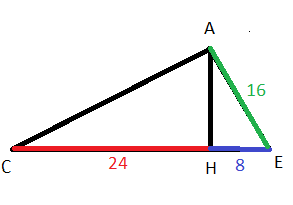
Fais un dessin
Dans le triangle EHA, on a EH = AE.cos(HEA)
cos(HEA) = EH/AH = 8/16 = 1/2 --> angle(HEA) = Pi/3vect(EH).vect(EA) = EH * EA * cos(HEA) = 8 * 16 * 1/2 = 64
Avec Pythagore, calcule AH² dans le triangle EHA.
Avec le résultat obtenu, par Pythagore dans le triangle AHC, calcule CA² (et donc CA)
Et en remarquant que HC = CA.cos(AHC)
... Il y a alors tout ce qu'il faut pour calculer : vect(CE).vect(CA)Il restera un petit effort à faire (pas bien grand) pour calculer vect(EA).vect(AC)
-
mtschoon dernière édition par mtschoon

Bonjour,
Méthode alternative possible,
Schéma (approximatif) revu avec les données de l'énoncé
AH2+HE2=AE2AH^2+HE^2=AE^2AH2+HE2=AE2 <=> AH2AH^2AH2=192 d'où AH=83AH=8\sqrt 3AH=83
AC2=AH2+HC2=768AC^2=AH^2+HC^2=768AC2=AH2+HC2=768 d'où AC=163AC=16\sqrt 3AC=163
@hugo-mt_22 , si tu connais la propriété de Projection (d'un des vecteurs sur l'autre) , tu peux l'utiliser.
Projection sur (CE) :
CE→.CA→=CE→.CH→=CE×CH\overrightarrow{CE}.\overrightarrow{CA}=\overrightarrow{CE}.\overrightarrow{CH}=CE\times CHCE.CA=CE.CH=CE×CH
Tu comptesProjection sur (EH) :
EH→.EA→=EH→.EH→=EH×EH=EH2\overrightarrow{EH}.\overrightarrow{EA}=\overrightarrow{EH}.\overrightarrow{EH}=EH\times EH=EH^2EH.EA=EH.EH=EH×EH=EH2
Tu comptesEA→.AC→\overrightarrow{EA}.\overrightarrow{AC}EA.AC peut se trouver, par exemple, avec les deux calculs précédents.
EA→.AC→=(EC→+CA→).AC→=EC→.AC→+CA→.AC→\overrightarrow{EA}.\overrightarrow{AC}=(\overrightarrow{EC}+\overrightarrow{CA}).\overrightarrow{AC}=\overrightarrow{EC}.\overrightarrow{AC}+\overrightarrow{CA}.\overrightarrow{AC}EA.AC=(EC+CA).AC=EC.AC+CA.AC
EA→.AC→=CE→.CA→−AC→.AC→\overrightarrow{EA}.\overrightarrow{AC}=\overrightarrow{CE}.\overrightarrow{CA}-\overrightarrow{AC}.\overrightarrow{AC}EA.AC=CE.CA−AC.AC
-
hugo.mt_22 dernière édition par
@mtschoon a dit dans Trigonométrie 1ère maths :
Donc,
EA . AC= -192-192 RACINE CARRE 3CE . CA= 4608 racine carré 3 + 13824
EH . EA= 64
-
@hugo-mt_22 Bonjour,
Vérifie les calculs.
Sauf erreur, l'énoncé précise que le point H est le pied de la hauteur issue du point A.
-
hugo.mt_22 dernière édition par
@Noemi Mais du coup, est ce que c'est bon?
-
Fais la figure et vérifie tes calculs, seul le dernier résultat est correct.
-
mtschoon dernière édition par mtschoon

@hugo-mt_22 , désolée, jai mal lu l'énoncé.
Tes écritures "en double" m'ont perturbée.J'ai refait la figure/pistes de calcul possibles, dans mon premier message.
-
BBlack-Jack dernière édition par
Je reprends mon approche :
Dans le triangle EHA, on a EH = AE.cos(HEA)
cos(HEA) = EH/AH = 8/16 = 1/2 --> angle(HEA) = Pi/3vect(EH).vect(EA) = EH * EA * cos(HEA) = 8 * 16 * 1/2 = 64
Avec Pythagore, calcule AH² dans le triangle EHA : AH² = AE² - HE² = 16² - 8² = 192
AH = 8*sqrt(3)Avec le résultat obtenu, par Pythagore dans le triangle AHC, calcule CA² (et donc CA)
CA² = AH² + CH²
CA² = 192 + 24² = 768
CA = 16*sqrt(3)Et en remarquant que HC = CA.cos(HCA)
... Il y a alors tout ce qu'il faut pour calculer : vect(CE).vect(CA)vect(CE).vect(CA) = CE.CA.cos(HCA) = CE.HC = (24+8)*24 = 768
Il restera un petit effort à faire (pas bien grand) pour calculer vect(EA).vect(AC)
On remarque que CE² = (24+8)² = 1024
Et que donc CE² = CA² + AE² (1024 = 768 + 16²) --> le triangle EAC est rectangle en A et angle CAE = 90°
---> vect(EA).vect(AC) = EA * AC * cos(CAE) = 0
Calculs non vérifiés.
-
mtschoon dernière édition par mtschoon

Re-bonjour,
Oui, @Black-Jack , tes calculs "non vérifiés" doivent être exacts, car avec la proposition que j'ai donnée, avec une méthode différente, j'obtiens, après calculs :
CE→.CA→=CE×CH=32×24=768\overrightarrow{CE}.\overrightarrow{CA}=CE\times CH=32\times 24=768CE.CA=CE×CH=32×24=768
AC→.AC→=AC2=768\overrightarrow{AC}.\overrightarrow{AC}=AC^2=768AC.AC=AC2=768D'où : EA→.AC→=768−768=0\overrightarrow{EA}.\overrightarrow{AC}=768-768=0EA.AC=768−768=0
(joli triangle EAC, rectangle en A)
-
hugo.mt_22 dernière édition par
@mtschoon merci grandement.
-
mtschoon dernière édition par

De rien @hugo-mt_22 , on fait au mieux...
A+