Première Générale - Probabilités
-
Noa Garcia dernière édition par
Exercice :
Une agence de sondage interroge les visiteurrs d'une exposition consacrée à l'Antiquité. La probabilité qu'une personne interrogée soit satisfaite par l'exposition est égale à 0,9
L'agence décide d'interroger 3 visiteurs de manière indépendante. On note X le nombre de visiteurs qui se déclarent satisfaits.
1- Déterminer la loi de probabilité de X.
2- Quelle est la probabilité d'interroger au moins une personne non satisfaite par l'exposition ?
-
@Noa-Garcia Bonjour,
Indique tes éléments de réponse.
Dessine un arbre pondéré de la situation.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Noa-Garcia , je regarde ton énoncé
@Noa-Garcia a dit dans Première Générale - Probabilités :
Une agence de sondage interroge les visiteurrs d'une exposition consacrée à l'Antiquité. La probabilité qu'une personne interrogée soit satisfaite par l'exposition est égale à 0,9
L'agence décide d'interroger 3 visiteurs de manière indépendante. On note X le nombre de visiteurs qui se déclarent satisfaits.
1- Déterminer la loi de probabilité de X.
2- Quelle est la probabilité d'interroger au moins une personne non satisfaite par l'exposition ?
La solution que tu dois indiquer dépend de l'avancée de ton cours...
Ici, l'expérience aléatoire est composée de 3 épreuves répétées indépendantes.
A chaque épreuve :
la probalilité d'un succés est p(S)=p=0.9p(S)=p=0.9p(S)=p=0.9 (personne satisfaite)
la probabilité d'un échec est p(S‾)=1−p=1−0.9=0.1p(\overline{S})=1-p=1-0.9=0.1p(S)=1−p=1−0.9=0.1 (personne non satisfaite)Soit XXX le nombre de succès sur les 3 épruves.
Si ton cours le permet, tu peux dire directement queXXX suit la loi binomiale B(n;p)B(n;p)B(n;p) , c'est à dire ici B(3;0.9)B(3;0.9)B(3;0.9)Toute l'explication est faite dans cette vidéo :
https://www.youtube.com/watch?v=xMmfPUoBTtMPour 0≤k≤30\le k\le 30≤k≤3, Pr(X=k)Pr(X=k)Pr(X=k)=(3k){3}\choose{k}(k3) 0.9k×0.13−k0.9^k\times 0.1^{3-k}0.9k×0.13−k
Si tu as besoin de passer par l'arbre pour faire les calculs (il y en a un dans la vidéo), je t'en joins un adapté à cet exercice :
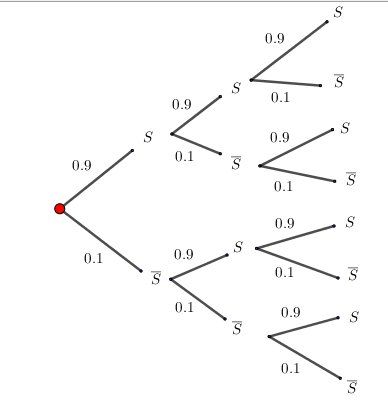
-
mtschoon dernière édition par mtschoon

@Noa-Garcia , pour la seconde question,
la probabilité d'interroger au moins une personne non satisfaite est la probabilité d'interroger au plus deux personnes satisfaites.
Tu dois donc calculer (avec l'arbre ou la formule )
Pr(X≤2)=Pr(X=0)+Pr(X=1)+Pr(X=2)Pr(X\le 2)=Pr(X=0)+Pr(X=1)+Pr(X=2)Pr(X≤2)=Pr(X=0)+Pr(X=1)+Pr(X=2)Le plus rapide est de passer par l'évènement contraire :
Pr(X≤2)=1−Pr(X=3)Pr(X\le 2)=1-Pr(X=3)Pr(X≤2)=1−Pr(X=3)Bons calculs.
Reposte si besoin.