produit scalaire 1ère

[hugo.mt_22]

Bonjour,

Soit ABCD un carré de centre O, avec AB = a

Déterminer AD→⋅OB→ en fonction de a.

[Noemi]

@hugo-mt_22 Bonjour,

Calcule les coordonnées des vecteurs AD et OB, puis le produit scalaire.

[mtschoon]

Bonsoir,

@hugo-mt_22 , tu peux calculer directement si tu préfères,

$AD=a$
la diagonale d'un carré de côté a est $a\sqrt{2}$ donc $OD=\frac{a\sqrt{2}}{2}$

$(\overrightarrow{AD},\overrightarrow{OB})=-\frac{3\pi }{4}$, tu en déduis le cosinus

$\overrightarrow{AD}.\overrightarrow{OB}=AD\times OB\times cos(-\frac{3\pi }{4})$ Tu comptes.

[hugo.mt_22]

@mtschoon cela fait -racine carré2 sur 2 a^2

[mtschoon]

@hugo-mt_22 , bonjour,

Pour plus de clarté, je te mets un schéma

Pour voir clairement l'angle, j'ai tracé $\overrightarrow{OE}=\overrightarrow{AD}$

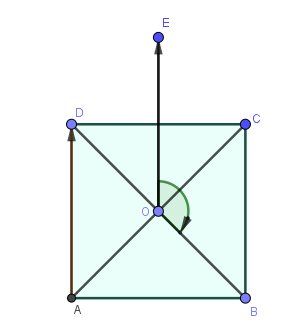
Je revois ta réponse (c'est presque ça, mais pas tout à fait)

[mtschoon]

@hugo-mt_22 ,

Tu dois calculer $a(\frac{a\sqrt{2}}{2})(-\frac{\sqrt{2}}{2})$

[hugo.mt_22]

@mtschoon cela fait -a^2/2

[mtschoon]

@hugo-mt_22 ,

c'est bon.