Dm de math produit scalaire

[Dauphin789]

ABCD est un parallelogramme, M, N, Q sont tels que :
DM = 4/5 DA AN= 3/4AB, CQ= 2/3 CD

La parallèle à (MQ) menée par N coupe (BC) en P. Il s'agit de trouver le coefficient k de colinéarité tel que BP = KAD. Considérons le repère (A, AB, AD).

1. Calculer les coordonnées des points M, N et Q.

2. Justifier que P a pour coordonnées (1; k).

3. En déduire que les vecteurs MQ et NP sont colinéaires et calculer k.

Dans cet exercice je parle de vecteur. Je n'arrive pas à là dernière question. Pourriez-vous m'aider s'il vous plaît ​

[Noemi]

@Dauphin789 Bonjour, (Marque de politesse à ne pas oublier !!)

Indique tes éléments de réponse la question qui te pose problème.
As-tu fait une figure ?

[mtschoon]

Bonjour,@Dauphin789

Comme Noemi te l'a indiqué, ici la politesse n'est pas une option.

Dans ton titre , tu parles de produit scalaire.

Je ne vois pas trop l'interêt du produit scalaire...

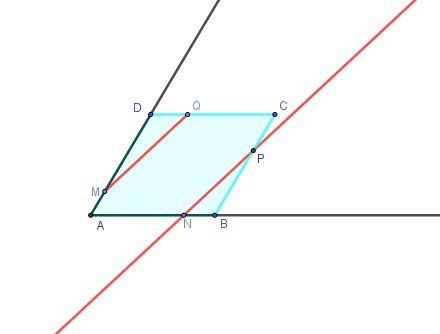
Pour la dernière question qui te gène , trouver $k$ (si j'ai bien lu), tu peux calculer les coordonnées des vecteurs colinéaires $\overrightarrow{MQ}$ et $\overrightarrow{NP}$

La condition pour que deux vecteurs de coordonnées $(X,Y)$ et $(X^{\prime },Y^{\prime })$ soient colinéaires est : $\boxed{X{Y}^{\prime }=Y{X}^{\prime }}$ que l'on peut aussi écrire $\boxed{X{Y}^{\prime }-Y{X}^{\prime }=0}$
Tu peux ainsi trouver $k$

Il y a cet exercice dans de nombreux endroits sur le web, par exemple ici .
http://lycee.lagrave.free.fr/IMG/pdf/Correction_1iereS._DM3.pdf

Tu peux ainsi vérifier tes réponses.

Reposte si tu n'y arrives pas.