Résolution d'une équation avec ln (Bloqué sur une question...)
-
CChris21300 dernière édition par Noemi
Bonjour, j'ai un problème sur la dernière question d'un exercice.
f(x) = ln(2x-1)-x+1
-
déterminer lim f(x) en 1/2 : pas de souci
-
déterminer lim f(x) en +oo : pas de souci
-
démontrez que f(x) =0 a 2 solutions : pas de souci
-
donnez valeur des 2 racines de f(x)... Là par contre problème...
J'ai commencé par :
ln(2x-1)-x+1 = 0
ln(2x-1)= x-1
e^(ln(2x-1)) = e^(x-1)
2x-1 = e^x / ee^x = e(2x-1)
e^x = 2ex- eEt là.. Bah je ne sais plus quoi faire...
Pourriez-vous juste me donner un indice me permettant de me lancer dans la bonne direction ?
Je vous remercie par avance pour votre aide
-
-
@Chris21300 Bonjour,
Une racine évidente : x=1x=1x=1, pour l'autre racine utilise la calculatrice pour avoir une valeur approchée.
-
mtschoon dernière édition par

Bonjour,
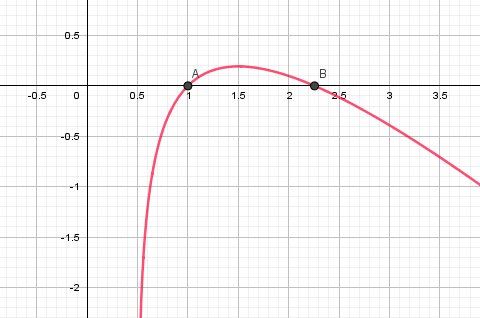
Illustration graphique
xA=1x_A=1xA=1
xB≈2.25x_B \approx 2.25xB≈2.25@Chris21300 , comme te l'a dit Noemi, utilise ta calculette (qui pourra te donner une meilleure précision)
-
CChris21300 dernière édition par
@Noemi bonjour et merci pour votre réponse,
En fait je ne souhaite pas faire une lecture directe mais trouver les réponses par le calcul
-
CChris21300 dernière édition par
@mtschoon bonjour et merci pour votre réponse mais en fait je souhaite trouver les réponses par le calcul

-
Avec la fonction indiquée, tu ne pourras pas trouver de valeur exacte.
-
CChris21300 dernière édition par
@Noemi donc je m'arrache les cheveux sur cette question depuis ce matin pour rien

Je pensais qu'il y avait un moyen de trouver la réponse par le calcul vu que la question du livre ne spécifiait par une évaluation par lecture directe...
Bon j'aurai au moins la satisfaction de ne pas être passé à côté d'une méthode permettant de calculer les valeurs exactes
Merci pour vos réponses
-
mtschoon dernière édition par mtschoon

Bonjour,
Effectivement @Chris21300 , la question de ton énoncé n'est pa détaillée.
En principe, après avoir prouvé (souvent par le TVI) qu'il existe une solution réelle dont on ne peut pas expliciter l'expression exacte numériquement, l'énoncé nomme cette solution, souvent avec la lettre α\alphaα.
Ensuite, il est demandé de trouver une valeur approchée de α\alphaα à 10−210^{-2}10−2 près, ou 10−310^{-3}10−3 près, ou 10−410^{-4}10−4 près, ...Si cela avait été écrit de cette façon, tu n'aurais pas eu de difficultés.