degré résoudre exercice

[hiba_mrcnn]

Bonjour peut-on m’aider à résoudre ce problème ?
Soit g un polynôme du second degré tel que 4 et -2
soient deux racines de g et tel que g (1)=12.
Déterminer g.

[Noemi]

@hiba_mrcnn Bonjour,

Si 4 est racine du polynôme c'est que $x-4$ est une facteur.
Si -2 est racine du polynôme c'est que $x+2$ est un facteur.
Soit $g(x)=a(x-4)(x+2)$
Détermine la valeur de $a$ à partir de $g(1)=12$.

[mtschoon]

Bonjour,

@hiba_mrcnn , vu que tu es en tout début d'année scolaire en Seconde, c'est difficile de savoir ce que tu sais sur le sujet...

$g(x)=a{x}^2+bx+c$ avec $a\ne 0$

Si a=tu as compris la démarche proposée par @Noemi pour trouver $a$ :
$g(x)=a(x-4)(x+2)$
donc $g(1)=a(1-4)(1+2)=-9a$
$g(1)=12$ <=> $-9a=12$ <=> $a=-\frac{4}{3}$

$g(x)=-\frac{4}{3}{x}^2+bx+c$

Pour déduire $b$ et $c$, tu peux, par exemple, résoudre par système :
$g(4)=0$ <=> $-\frac{4}{3}\times 4^2+4x+c=0$
$g(4-2=0$ <=> $-\frac{4}{3}\times (-2{)}^2-2b+c=0$

Tu simplifies un peu chaque équation.
Tu résous ce système d' inconnues $b$ et $c$
Après calculs, tu dois trouver : $b=\frac{8}{3}$ et $c=\frac{32}{3}$

Conclusion :
$\boxed{g(x)=-\frac{4}{3}{x}^2+\frac{8}{3}x+\frac{32}{3}}$

Bons calculs.

Remarques :

Si ton cours te donne les expressions des coordonnées du sommet de la parabole représentative de $g$, tu peux les utiliser connaissant $a$, pour trouver $b$ et $c$ , car les valeurs sont très adaptées.

Tu peux aussi solutionner tout l'exercice en écrivant $g(x)=a{x}^2+bx+c$ et en résolvant le système d'inconnues $a$, $b$, $c$ :
$\{\begin{array}{l}g(4)=0\\ g(-2)=0\\ g(1)=12\end{array}$

En bref, tu as le choix !

[mtschoon]

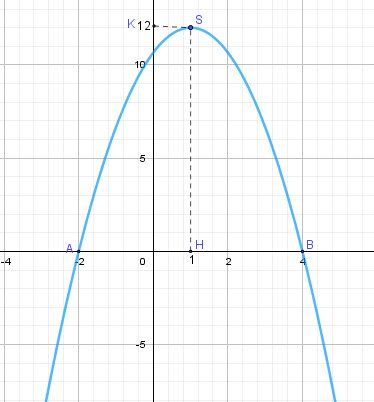
Représentation graphique de $g$
$A(-2,0)$
$B(4,0)$
$S(1,12)$