Progression Arithmétique

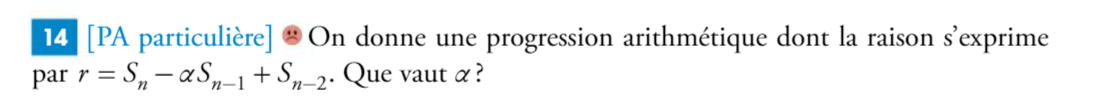
Hello Hello, navré si je suis pas au bon endroit mais quelqu'un aurait un petit coup de main à donner ?

Bonjour,

Sûr de l'énoncé ?

S(n-1) = S(n) - r
S(n-2) = S(n) - 2r

r = S(n) - alpha.(S(n) - r) + S(n) - 2r

r(3 - alpha) = S(n) * (2 - alpha)

Si on présume qu'on cherche une valeur de alpha constante, comme r est constante, la suite doit être constante et donc r = 0 et alpha = 2

Une suite constante est bien arithmétique (raison : r = 0), elle est aussi géométrique (raison q = 1)

Sauf si j'ai mal interprété l'énoncé.

Merci de ta réponse !

Concernant l'énoncé, j'espère, je l'ai screenshot du manuel (mais connaissant mon prof, il fait parfois des erreurs).

Je comprends bien ton raisonnement mis à part peut-être la base. Pourquoi S(n-1) = S(n) - r ? C'est peut-être basique comme question, mais je peine à comprendre.

Pour une progression arithmétique de terme Sn , on a la relation S(n+1) = S(n) + r avec r la raison qui est une constante.

on a donc un terme de la progression = le terme précédent de la progression + r

ou ce qui revient au même : un terme de la progression = le terme suivant de la progression - r

Ce ce qui est exprimé par S(n-1) = S(n) - r

puisque S(n-1) est un terme de la progression et S(n) est le terme suivant de la progression.

Je suis d'accord si on parle de terme de la progression pour S(n). Mais S(n) n'est pas la sommation de la progression ?

@Black-Jack

Si on présume qu'on cherche une valeur de alpha constante, comme r est constante, la suite doit être constante et donc r = 0 et alpha = 2

Je comprends donc le raisonnement par lequel tu es arrivé à cette étape. Maintenant, je comprends pas bien comment tu en déduis que r = 0 et alpha = 2.

Bonjour,

@Joël-Aubry , ici , les scans d'énoncés ne sont pas autorisés (sauf pour tableaux ou graphiques).

Regarde les consignes avant de poster
https://forum.mathforu.com/topic/1383/stop-lire-ce-sujet-tu-devras-avant-de-poster-ton-message

Je te conseille de re-écrire ta question de départ en effaçant le scan et en écrivant la question à la main (mode Edition)
(tu n'as que deux lignes à écrire...)

En principe la modération efface les scans d'énoncés, avant qu'il y ait des réponses.

Je viens juste de regarder cet exercice et n'ai rien cherché mais j'ai un doute sur l'interprétation donnée.

De façon usuelle, $S_n$ ne représente pas le terme général d'une suite arithmétique mais la somme des n premiers termes. Regarde les notations de ton cours.

Ainsi, en considérant que le premier terme est $U_1$ :
$Sn=U1+Un2S_n=\dfrac{U_1+U_n}{2}$
$Sn−1=U1+Un−12S_{n-1}=\dfrac{U_1+U_{n-1}}{2}$
$Sn−2=U1+Un−22S_{n-2}=\dfrac{U_1+U_{n-2}}{2}$

Tu peux bien sûr exprimer $U_n$ , $U_{n-1}$ et $U_{n-2}$ en fonction de la raison $r$

A toi de voir.

@mtschoon

Mille excuses, il est vrai que dans la hâte je n'ai pas pensé à regarder les règles. Je ne peux malheureusement pas éditer le post Mais sitôt que j'aurais compris, j'effacerai le post directement.

Merci pour toutes les réponses. J'ai le même problème concernant l'écriture usuelle du Sn. Saurais-tu résoudre cet exercice du coup ?

La réponse est bel et bien alpha = 2. Mais je n'ai pas le développement .

@Joël-Aubry Bonjour,

Il n'est pas apprécié d'effacer son post après avoir obtenu des réponses. C'est contraire à l'un des objectifs de ce forum.

C'est dommage que des réponses aient été données à un sujet scanné. Le scan du sujet étant interdit sur ce forum. Seuls les scans de figures, schémas ou graphiques sont autorisés.

@Joël-Aubry , bonsoir,

C'est dommage que tu n'aies pas pu éditer ton premier post pour supprimer ton scan et écrire l'énoncé à la place.

Je m'associe à tout ce qu'a indiqué @Noemi .
En particulier, il ne faut pas supprimer le premier post après avoir obtenu des réponses !
Cela empêcherait de comprendre la question, ce qui ne serait pas normal, car ici, tu es sur un forum public et tout consultant doit pouvoir comprendre.

Pour en revenir à ta question, si tu fais les calculs avec $S$ voulant dire "somme" comme je te l'ai proposé, tu obtiendras encore le cas trivial : $α=2\alpha=2$ et $r = 0$

Cet exercice me semble bizarre...