le produit scalaire et les vecteurs

bonjour,
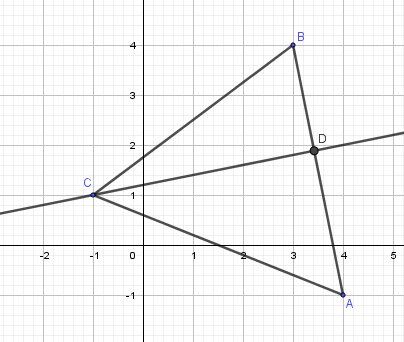
je n'arrive pas à justifier ça: Soit D le projeté orthogonal du point C sur la droite (AB), justifier que le vecteur AB fois le vecteur AD et égale au Vecteur AB fois le vecteur AC
les seuls info que j 'ai c'est les coordonnée des point A,B et
A(4,-1) , B(3,4) et C (-1,1)

@Agnès-quintil Bonjour,

Une piste :
Détermine les coordonnées du point $D$ , puis calcule les produits scalaires.

bonjour,
je n'ai aucune information pour en déduire les coordonnées de D et le seul produit scalaire que j'ai calculer avec le vecteur AB et le vecteur AC est j'ai trouvé 15 car les coordonnée du vecteur AB (-1,5) et les coordonnées du vecteur AC (-5,2)

@Agnès-quintil

Le point $D$ est le projeté orthogonal du point $C$ sur la droite $(A B)$ , donc le point $D$ appartient à la droite $(A B)$ et les droites $(C D)$ et $(A B)$ sont perpendiculaires.

bonjour,
vous pensez que si je le justifie avec la règle du parallélogramme qui est le vecteur AB + le vecteur AC donnent le vecteur AD

@Agnès-quintil

Détermine l'équations des droites $(A B)$ et $(C D)$ puis les coordonnées du point d'intersection $D$ de ces deux droites.

Bonjour,

@Agnès-quintil , cette question est peut-être la première de ton exercice car on peut y répondre sans rien faire (ou presque...)

Tu peux bien sûr faire les calculs avec les coordonnées,vu que tu les donnes, mais c'est bien long....

La question posée fait partie des propriétés du produit scalaire
(théorème relatif à la projection).
Tu le trouves ici au I paragraphe 3.
https://www.mathforu.com/premiere-s/produit-scalaire-et-applications-en-1ere-s/
Si tu connais cette propriété, il te suffit de l'appliquer.

Tu peux aussi transformer avec la relation de Chasles :
$AB→.AC→=AB→(AD→+DC)→\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}(\overrightarrow{AD}+\overrightarrow{DC)}$

$AB→.AC→=AB→.AD→+AB→.DC→\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AB}.\overrightarrow{DC}$

$AB→.DC→=0\overrightarrow{AB}.\overrightarrow{DC}=0$ car vecteurs orthogonaux, d'où la réponse souhaitée $AB→.AC→=AB→.AD→\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}.\overrightarrow{AD}$

Mais, à quoi bon donner les coordonnées des points (sauf si elles sont utiles à une question suivante) ?

@mtschoon merci mais après avoir justifier ca il faut que je trouve la distance AD

@Agnès-quintil , tu as le choix

Tu peux faire avec les équations de droites comme te l'a indiqué @Noemi .

Tu peux faire exclusivement avec l'égalité que tu viens de démontrer.
Tu peux écrire :

$AB→.AC→=AB×AD\overrightarrow{AB}.\overrightarrow{AC}=AB\times AD$

Donc : $AD=AB→.AC→ABAD=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{AB}$

Connaissant les coordonnées de $A, B, C$ , tu peux calculer le numérateur et le dénominateur et tu obtiens $A D$

@Noemi je n'arrive pas a déterminer les équations des droites AB at CD

@Agnès-quintil , en attendant que @Noemi te réponde, je te précise la piste que je t'ai indiquée

$AB→\overrightarrow{AB}$ a pour coordonnées $(3 - 4, 4 + 1) = (- 1, 5)$
$AC→\overrightarrow{AC}$ a pour coordonnées $(- 1 - 4, 1 + 1) = (- 5, 2)$

$AB→.AC→=(−1)(−5)+(5)(2)\overrightarrow{AB}.\overrightarrow{AC}=(-1)(-5)+(5)(2)$

$AB=(3−4)2+(4+1)2AB=\sqrt{(3-4)^2+(4+1)^2}$

Après calculs, avec la formule que je t'ai donnée, tu as $A D$

merci je vous retient au courant si je coince a une question

@Agnès-quintil

Pour l'équation de la droite $(A B)$ , tu peux utiliser les coordonnées des points $A$ et $B$ .
Regarde ce cours : https://www.mathforu.com/seconde/determiner-equation-droite/
Pour l'équation de la droite $(C D)$ , tu peux utiliser le produit scalaire avec les vecteurs orthogonaux.

@Agnès-quintil ,

Quelle que soit ta méthode, tu dois trouver :

$AD=1526AD=\dfrac{15}{\sqrt{26}}$

$AD≈2.94AD\approx 2.94$

Bons calculs.

moi je trouve pour AD : -5 divisé par racine de 6

r

c'est bon j'ai trouvé mon erreur par contre je n'arrive pas au suivante question qui sont :
. déterminer la hauteur du triangle ABC issue de C
. calculer l'aire du triangle ABC

@Agnès-quintil , bonjour,

Pistes,

La hauteur issue de C au triangle (ABC) est (CD)

Tu peux calculer CD avec le théorème de Pythagore

$CD^2+AD^2=AC^2$ <=> $CD^2=AC^2-AD^2$

$CD=AC2−AD2CD=\sqrt{AC^2-AD^2}$

Tu connais $A D$ donc tu peux connaître $AD^2$
Tu peux calculer $A C$ , même directement $AC^2$

$AC^2=(x_C-x_A)^2+(y_C-y_A)^2$

Ainsi, tu peux obtenir $C D$

$aire(ABC)=base×hauteur2aire(ABC)=\dfrac{base\times hauteur}{2}$

$aire(ABC)=AB×CD2aire(ABC)=\dfrac{AB\times CD}{2}$

Bons calculs.

@mtschoon merci

@mtschoon j'ai trouvé pour CD= racine de -8.5 et pour l'aire de ABC =-3.57
est ce normal comme résultat ou pas

@Agnès-quintil ,

Non , ce n'est pas normal car ces valeurs ne peuvent pas être négatives et on ne peut pas, dans $R$ , prendre la racine carrée d''un nombre négatif.

Pour $C D$ tu dois trouver :
$CD=2326CD=\dfrac{23}{\sqrt{26}}$
$CD≈4.51CD\approx 4.51$

Evidemment , dans le calcul de l'aire, il y aura une simplification par $26\sqrt{26}$ et l'aire vaudra exactement 11.5 (en unités d'aire).

Recompte tes calculs.

je ne trouve pas mon erreur car j'ai fait AC au carré qui vaut 29 et AD au carré qui vaut 15/racine de 6 au carré et je trouve toujours racine de -8.5

@Agnès-quintil a dit dans le produit scalaire et les vecteurs :

je ne trouve pas mon erreur car j'ai fait AC au carré qui vaut 29 et AD au carré qui vaut 15/racine de 6 au carré et je trouve toujours racine de -8.5

Bonjour,

$AD2=(1526)2AD^2 = (\frac{15}{\sqrt{26}})^2$

et pas : $AD2=(156)2AD^2 = (\frac{15}{\sqrt{6}})^2$

@Black-Jack merci

@Agnès-quintil

C'est bien ce que je t'avais indiqué :

@mtschoon a dit dans le produit scalaire et les vecteurs :

@Agnès-quintil ,

Quelle que soit ta méthode, tu dois trouver :

$AD=1526AD=\dfrac{15}{\sqrt{26}}$

$AD≈2.94AD\approx 2.94$

Bons calculs.

oui c'est juste moi qui est mal taper a ma calcutrice j'ai racine de 6 au lieu d racine 26

@Agnès-quintil ,
OK.
Si c'est seulement un problème de calculatrice, ce n'est pas grave.
L'essentiel est que tu aies compris.
Bon travail.