Maths limite fonction

Bonjour j’ai presque fini mon dm de math et il me reste juste deux question à faire si quelqu’un pourrait m’aider svp .
Je dois calculer les limites de la fonction : $4x2+3x+11−x2\dfrac{4x^2+3x+1}{1-x^2}$

Ecriture de la fonction mise en Latex par la modération du forum.

@Tom-let Bonjour,

Les limites pour quelles valeurs de $x$ ?
En $±∞±\infty$ , mets $x^2$ en facteur au numérateur et dénominateur.
En $- 1$ et $1$ , cherche dans chaque cas, les limites pour la valeur supérieure et la valeur inférieure.

Indique des calculs et/ou résultats si tu souhaites une vérification.

Bonjour,

@Tom-let , pour vérifier tes limites (lorsque tu les auras trouvées) je te joins la représentation graphique de la fonction avec les asymptotes

En rouge : asymptote horizontale d'équation $y = - 4$
En noir : asymptotes verticales d'équations $x = - 1$ et $x = 1$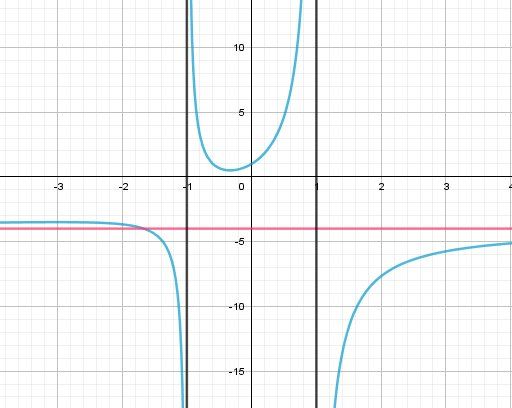

Comme te l'a indiqué @Noemi , reposte si besoin pour trouver les limites.

@mtschoon ok merci beaucoup et ensuite je doit trouver la position relative de la courbe représentative de f et de la droite To ?
Et To j’ai trouver 1x+3
Mais après je sais pas quoi faire faire

@Tom-let

Etudie le signe de $f(x)-T_0(x)$

@Noemi oui mais c’est après cela que je n’arrive pas mais je sais que je doit trouver les valeur de x pour lesquelles Cf est en dessous deTo et les valeurs de x pours lesquelles Cf est au dessus de To

@Noemi finalement est ce que chest bien pour x en dessous ou au dessus de -5/3 que le signe change ?

@Tom-let

A quoi correspond la droite $T_0$ ?
$f(x)−T0(x)=4x2+3x+11−x2−(x+3)=.....f(x)-T_0(x)= \dfrac{4x^2+3x+1}{1-x^2}-(x+3)= .....$

Bonjour,

J'aurais pensé que $T_0)$ était la tangente à la courbe au point d'abscisse 0, vu la notation, mais ce n'est pas ça car la tangente à la courbe au point d'abscisse 0 a pour équation $y = 3 x + 1$ alors que @Tom-let parle de $y = x + 3$ (sauf s'il s'est trompé...)