étudier une fonction
-
AAgnès quintil dernière édition par
bonjour,
soit la fonction f(x)=3x-1/1-5x définie sur son ensemble de définition Df. et on me pose comme première question donner Df sauf que je ne vois pas comment le donner car c'est une u/v et une u/v est définie sur un intervalle donc je ne sais pas comment trouver l'intervalle pouvez vous m'aider s'il vous plaît
-
mtschoon dernière édition par mtschoon

@Agnès-quintil , bonsoir,
Si c'est bien f(x)=3x−11−5xf(x)=\dfrac{3x-1}{1-5x}f(x)=1−5x3x−1 (sans Latex, tu aurais dû mettre des parenthèses pour séparer numérateur et dénominateur)
Condition d'existence : 1−5x≠01-5x\ne 01−5x=0 (on ne peut pas diviser par 0)
−5x≠−1-5x\ne -1−5x=−1 <=> x≠−1−5x\ne\dfrac{-1}{-5}x=−5−1 <=> x≠15x\ne \dfrac{1}{5}x=51
L'ensemble DfDfDf de définition est donc RRR privé de {15\dfrac{1}{5}51}
Tu peux écrire cet ensemble comme union de deux intervalles :
Df=]−∞,15[∪]15,+∞[Df=]-\infty,\dfrac{1}{5}[\cup]\dfrac{1}{5},+\infty[Df=]−∞,51[∪]51,+∞[
-
AAgnès quintil dernière édition par
merci oui désolé j'ai zappé de mettre les parenthèse
-
AAgnès quintil dernière édition par
bonsoir ,
je n'arrive pas a étudier les limites de la fonction aux bornes de son ensemble de définition et donner les asymptotes éventuelles
pouvez m'aider s'il vous plaît
-
@Agnès-quintil Bonsoir,
Un exemple à étudier et appliquer : http://maths.enligne.free.fr/limite/limite_inf_rati.htm
-
mtschoon dernière édition par

Bonsoir,
@Agnès-quintil , j'espère qu'avec l'exemple donné par @Noemi , tu vas arriver à trouver les limites que tu cherches, sinon reposte.
Remarque : tu as dû te tromper de rubrique car cet exercice est un exercice de Première plutôt que de Terminale .
D'ailleurs , tu avais mis ton exercice sur le produit scalaire en rubrique Première.
Peut-être que la modération le déplacera.
-
mtschoon dernière édition par

Bonjour,
Merci à la modération d'avoir déplacer ce topic.
-
mtschoon dernière édition par

@Agnès-quintil , bonjour,
Pour pouvoir vérifier tes réponses (que tu as dû trouver, j'espère, avec le lien donné) , je te joins les résultats.
Ce ne sont que les résultats, il faut tout démontrer.
limx→−∞=−35\displaystyle \lim_{x\to -\infty}=-\dfrac{3}{5}x→−∞lim=−53limx→+∞=−35\displaystyle \lim_{x\to +\infty}=-\dfrac{3}{5}x→+∞lim=−53
limx→15(x<15)=−∞\displaystyle \lim_{x\to \dfrac{1}{5} (x\lt \dfrac{1}{5})}=-\inftyx→51(x<51)lim=−∞
limx→15(x>15)=+∞\displaystyle \lim_{x\to \dfrac{1}{5} (x\gt \dfrac{1}{5})}=+\inftyx→51(x>51)lim=+∞
Illustration graphique (que tu peux obtenir sur ta calculette)
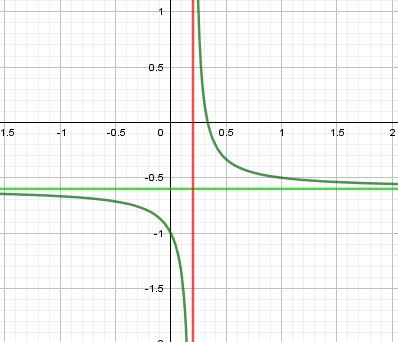
La courbe est en bleu
L'asymptote horizontale d'équation y=−35y=-\dfrac{3}{5}y=−53 est en vert
L'asymptote verticale d'équation x=15x=\dfrac{1}{5}x=51 est en rougeBonnes démonstrations.
Reposte si besoin.
-
AAgnès quintil dernière édition par
@mtschoon merci
-
AAgnès quintil dernière édition par
je ne sais pas quel méthode utiliser pour étudier le sens de variation de f soit avec les limites ou avec la dérivé
-
mtschoon dernière édition par mtschoon

Pour trouver le sens de variation d'une fonction, tu calcules la dérivée et tu cherches son signe.
Si ton cours sur la dérivation n'est pas clair, tu peux consulter ici :
https://www.maths-et-tiques.fr/telech/DerivTS.pdf
-
mtschoon dernière édition par

Piste,
Après calculs (dérivée d'un quotient), tu dois trouver :
f′(x)=−2(5x−1)2f'(x)=\dfrac{-2}{(5x-1)^2}f′(x)=(5x−1)2−2Tu tires la conclusion sur signe de f′(x)f'(x)f′(x) et sens de variation de fff, sur chacun des intervalles]−∞,15[]-\infty,\dfrac{1}{5}[]−∞,51[ et ]15,+∞[]\dfrac{1}{5}, +\infty[]51,+∞[